| NCERT Exemplar Solutions | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Solved Examples (Examples 1 to 17) | Question 1 to 30 (Multiple Choice Questions) | Question 31 to 71 (Fill in the Blanks) |
| Question 72 to 108 (True or False) | Question 109 to 136 | |
Chapter 1 Integers
Welcome to this dedicated resource offering meticulously detailed, step-by-step solutions and comprehensive explanations for the NCERT Exemplar problems tailored for Class 7 Mathematics, Chapter 1: Integers. It's crucial to understand that these Exemplar questions are purposefully designed to push students beyond the basic operational proficiency typically covered in standard textbook exercises. The primary objective is to cultivate a significantly deeper understanding of the integer system, focusing intently on the fundamental properties of integers, developing advanced problem-solving techniques for complex scenarios, and fostering higher-order thinking skills essential for mathematical growth.
The solutions provided herein encompass the complete spectrum of Class 7 integer topics. This includes not only a rigorous review of the four fundamental operations – addition, subtraction, multiplication, and division – involving integers, but also places a strong, consistent emphasis on mastering the critical sign rules associated with each operation. More significantly, these solutions delve deeply into the structural characteristics of integers by exploring their behaviour under these operations. Key properties covered in detail include:
- Closure Property: Whether performing an operation on two integers always results in an integer.
- Commutativity: Whether the order of operands affects the result (e.g., Is $a + b = b + a$? Is $a \times b = b \times a$?).
- Associativity: Whether the grouping of operands affects the result (e.g., Is $(a + b) + c = a + (b + c)$? Is $(a \times b) \times c = a \times (b \times c)$?).
- Existence of Identities: Recognizing the Additive Identity ($0$, since $a + 0 = a$) and the Multiplicative Identity ($1$, since $a \times 1 = a$).
- Additive Inverse: Understanding that for every integer $a$, there exists $-a$ such that $a + (-a) = 0$.
- The vitally important Distributive Property of multiplication over addition ($a \times (b + c) = (a \times b) + (a \times c)$) and subtraction ($a \times (b - c) = (a \times b) - (a \times c)$).
A major focus of the Exemplar problems, and therefore these solutions, is demonstrating how to apply these properties strategically. Many problems require simplifying complex numerical expressions efficiently by using properties like distributivity, rather than resorting to lengthy, brute-force calculations. The solutions clearly illustrate these intelligent applications step-by-step.
The diverse range of question formats found in the NCERT Exemplar is fully addressed: Multiple Choice Questions (MCQs) designed to test precise understanding of rules and properties; Fill-in-the-Blanks requiring specific numerical answers or correct terminology; True/False statements probing conceptual clarity and exposing common misconceptions about integer behaviour; and comprehensive Short/Long Answer questions. These latter types often demand detailed calculations, simplification of expressions involving multiple steps, nested brackets, and various operations, or the careful solving of intricate word problems. Such word problems frequently involve real-world scenarios like tracking temperature fluctuations, calculating changes in elevation above/below sea level, determining final scores in games with points and penalties, or managing financial transactions involving profit and loss (sometimes requiring calculations with $\textsf{₹}$). The provided solutions meticulously break down these complex problems into understandable, manageable steps, clearly explaining the logical reasoning behind applying specific properties or rules, justifying answers particularly for conceptual True/False questions, and highlighting potential pitfalls, especially concerning sign errors during calculations. This resource is invaluable for any student aiming to achieve mastery over integer operations, appreciate their underlying structure through properties, significantly enhance their problem-solving capabilities for challenging situations, and build an unshakeable foundation for future algebraic studies.
Solved Examples (Examples 1 to 17)
In Examples 1 to 3, there are four options, out of which one is correct. Write the correct answer.
Example 1: Madhre is standing in the middle of a bridge which is 20 m above the water level of a river. If a 35 m deep river is flowing under the bridge (see Fig. 1.1), then the vertical distance between the foot of Madhre and bottom level of the river is:
(a) 55 m
(b) 35 m
(c) 20 m
(d) 15 m
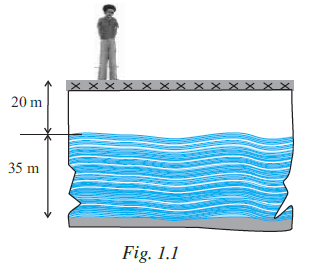
Answer:
Given:
Height of the bridge above the water level = $20 \text{ m}$
Depth of the river = $35 \text{ m}$
To Find:
The vertical distance between the foot of Madhre and the bottom level of the river.
Solution:
Madhre is standing in the middle of the bridge, which means their foot is at the level of the bridge deck.
The vertical distance between the foot of Madhre (at the bridge level) and the bottom level of the river is the sum of the height of the bridge above the water level and the depth of the river.
Vertical distance = Height of bridge above water level + Depth of river
Vertical distance = $20 \text{ m} + 35 \text{ m}$
Vertical distance = $55 \text{ m}$
The vertical distance between the foot of Madhre and the bottom level of the river is $55 \text{ m}$.
This matches option (a).
The correct answer is (a) 55 m.
Example 2: [(– 10) × (+ 9)] + ( – 10) is equal to
(a) 100
(b) –100
(c) – 80
(d) 80
Answer:
Solution:
We need to evaluate the expression $[(- 10) \times (+ 9)] + ( - 10)$.
First, evaluate the expression inside the square brackets:
$(- 10) \times (+ 9)$
When multiplying a negative integer by a positive integer, the result is a negative integer.
$(- 10) \times (+ 9) = - (10 \times 9) = -90$
Now, substitute this result back into the original expression:
$[-90] + (- 10)$
Adding a negative number is the same as subtracting the corresponding positive number.
$-90 + (-10) = -90 - 10$
When subtracting a positive number from a negative number, or adding two negative numbers, we add their absolute values and keep the negative sign.
$90 + 10 = 100$
So, $-90 - 10 = -100$
Thus, $[(- 10) \times (+ 9)] + ( - 10) = -100$.
This matches option (b).
The correct answer is (b) –100.
Example 3: –16 ÷ [8 ÷ (–2)] is equal to
(a) –1
(b) 1
(c) 4
(d) –4
Answer:
Solution:
We need to evaluate the expression $-16 \div [8 \div (-2)]$.
First, evaluate the expression inside the square brackets using the order of operations (PEMDAS/BODMAS):
$[8 \div (-2)]$
When a positive integer is divided by a negative integer, the result is a negative integer.
$8 \div (-2) = -(8 \div 2) = -4$
Now, substitute this result back into the original expression:
$-16 \div [-4]$
When a negative integer is divided by a negative integer, the result is a positive integer.
$-16 \div (-4) = +(16 \div 4) = 4$
Thus, $-16 \div [8 \div (-2)] = 4$.
This matches option (c).
The correct answer is (c) 4.
In Examples 4 and 5, fill in the blanks to make the statements true.
Example 4: (– 25) × 30 = – 30 × _______.
Answer:
Solution:
The given equation is $(– 25) \times 30 = – 30 \times \text{_______}$.
Let the missing number in the blank be $x$.
So, we have the equation:
$(-25) \times 30 = -30 \times x$
First, calculate the product on the left side:
$(-25) \times 30 = -750$
Now the equation becomes:
$-750 = -30 \times x$
To find the value of $x$, divide both sides of the equation by $-30$:
$x = \frac{-750}{-30}$
$x = \frac{750}{30}$
$x = \frac{75}{3}$
$x = 25$
Thus, the statement becomes $(– 25) \times 30 = – 30 \times 25$, which is true as both sides are equal to $-750$.
The number to fill in the blank is $25$.
Example 5: 75 ÷ _______ = – 75
Answer:
Solution:
The given equation is $75 \div \text{_______} = – 75$.
Let the missing number in the blank be $x$.
So, we have the equation:
$75 \div x = -75$
We can rewrite the division as a fraction:
$\frac{75}{x} = -75$
To solve for $x$, we can multiply both sides by $x$ (assuming $x \neq 0$):
$75 = -75 \times x$
Now, divide both sides by $-75$:
$x = \frac{75}{-75}$
$x = -1$
Thus, the statement becomes $75 \div (-1) = -75$, which is true.
The number to fill in the blank is $-1$.
In Examples 6 and 7, state whether the statements are True or False.
Example 6: (–5) × (–7) is same as (–7) × (–5)
Answer:
Statement:
$(–5) \times (–7)$ is same as $(–7) \times (–5)$.
Solution:
We need to check if the product of $(-5)$ and $(-7)$ is equal to the product of $(-7)$ and $(-5)$.
Consider the left side of the comparison:
$(-5) \times (-7)$
The product of two negative integers is a positive integer.
$(-5) \times (-7) = 5 \times 7 = 35$
Consider the right side of the comparison:
$(-7) \times (-5)$
The product of two negative integers is a positive integer.
$(-7) \times (-5) = 7 \times 5 = 35$
Since $35 = 35$, the statement $(–5) \times (–7) = (–7) \times (–5)$ is true.
This equality illustrates the commutative property of multiplication for integers, which states that for any two integers $a$ and $b$, $a \times b = b \times a$.
Conclusion:
The statement is True.
Example 7: (– 80) ÷ (4) is not same as 80 ÷ (–4)
Answer:
Statement:
$(– 80) \div (4)$ is not same as $80 \div (–4)$.
Solution:
We need to evaluate both expressions and compare their results.
Consider the left side of the comparison:
$(-80) \div (4)$
When a negative integer is divided by a positive integer, the result is a negative integer.
$(-80) \div (4) = -(80 \div 4) = -20$
Consider the right side of the comparison:
$80 \div (-4)$
When a positive integer is divided by a negative integer, the result is a negative integer.
$80 \div (-4) = -(80 \div 4) = -20$
Comparing the results, we have:
Left side result: $-20$
Right side result: $-20$
Since $-20 = -20$, the statement $(– 80) \div (4)$ is the same as $80 \div (–4)$.
The given statement claims that the results are *not* the same, which is false.
Conclusion:
The statement is False.
Example 8: Find the odd one out of the four options in the following:
(a) (–2, 24)
(b) (–3, 10)
(c) (–4, 12)
(d) (–6, 8)
Answer:
Solution:
We are given four pairs of integers and need to find the one that does not fit a pattern shared by the others.
Let's examine a possible relationship between the two numbers in each pair, such as their product.
For option (a):
The product of the integers is $(-2) \times 24$.
$(-2) \times 24 = -48$
For option (b):
The product of the integers is $(-3) \times 10$.
$(-3) \times 10 = -30$
For option (c):
The product of the integers is $(-4) \times 12$.
$(-4) \times 12 = -48$
For option (d):
The product of the integers is $(-6) \times 8$.
$(-6) \times 8 = -48$
We can see that the product of the integers in options (a), (c), and (d) is $-48$.
The product of the integers in option (b) is $-30$, which is different from the others.
Therefore, the pair (–3, 10) is the odd one out.
The correct answer is (b) (–3, 10).
Example 9: Find the odd one out of the four options given below:
(a) (–3, –6)
(b) (+1, –10)
(c) (–2, –7)
(d) (–4, –9)
Answer:
Solution:
We are given four pairs of integers and need to find the one that does not fit a pattern shared by the others.
Let's examine a possible relationship between the two numbers in each pair, such as their product.
For option (a):
The product of the integers is $(-3) \times (-6)$.
$(-3) \times (-6) = 18$
For option (b):
The product of the integers is $(+1) \times (-10)$.
$(+1) \times (-10) = -10$
For option (c):
The product of the integers is $(-2) \times (-7)$.
$(-2) \times (-7) = 14$
For option (d):
The product of the integers is $(-4) \times (-9)$.
$(-4) \times (-9) = 36$
Let's consider another possible pattern, such as the sign of the integers in each pair.
In option (a), both integers are negative ($(-), (-)$).
In option (b), the first integer is positive and the second is negative ($+, (-)$).
In option (c), both integers are negative ($(-), (-)$).
In option (d), both integers are negative ($(-), (-)$).
Options (a), (c), and (d) consist of pairs where both integers are negative.
Option (b) consists of a pair where one integer is positive and the other is negative.
Therefore, the pair (+1, –10) is the odd one out based on the signs of the integers in the pair.
The correct answer is (b) (+1, –10).
Example 10: Match the integer in Column I to an integer in Column II so that the sum is between –11 and – 4
Column I
(a) –6
(b) +1
(c) +7
(d) –2
Column II
(i) –11
(ii) –5
(iii) +1
(iv) –13
Answer:
Solution:
We need to match an integer from Column I with an integer from Column II such that their sum lies strictly between $-11$ and $-4$. This means the sum must be greater than $-11$ and less than $-4$, i.e., in the range $(-11, -4)$. The possible integer sums in this range are $-10, -9, -8, -7, -6, -5$.
Let's find the sum for each possible combination of an integer from Column I and an integer from Column II:
From Column I (a) $-6$ with integers in Column II:
$-6 + (-11) = -17$
$-6 + (-5) = -11$
$-6 + (+1) = -5$
$-6 + (-13) = -19$
The sum $-5$ is between $-11$ and $-4$. So, (a) matches with (iii).
From Column I (b) $+1$ with integers in Column II:
$+1 + (-11) = -10$
$+1 + (-5) = -4$
$+1 + (+1) = +2$
$+1 + (-13) = -12$
The sum $-10$ is between $-11$ and $-4$. So, (b) matches with (i).
From Column I (c) $+7$ with integers in Column II:
$+7 + (-11) = -4$
$+7 + (-5) = +2$
$+7 + (+1) = +8$
$+7 + (-13) = -6$
The sum $-6$ is between $-11$ and $-4$. So, (c) matches with (iv).
From Column I (d) $-2$ with integers in Column II:
$-2 + (-11) = -13$
$-2 + (-5) = -7$
$-2 + (+1) = -1$
$-2 + (-13) = -15$
The sum $-7$ is between $-11$ and $-4$. So, (d) matches with (ii).
The matches are:
(a) –6 matches with (iii) +1 (Sum = -5)
(b) +1 matches with (i) –11 (Sum = -10)
(c) +7 matches with (iv) –13 (Sum = -6)
(d) –2 matches with (ii) –5 (Sum = -7)
Example 11: If a is an integer other than 1 and –1, match the following:
Column I
(a) a ÷ (–1)
(b) 1 ÷ (a)
(c) (–a) ÷ (–a)
(d) a ÷ (+1)
Column II
(i) a
(ii) 1
(iii) Not an integer
(iv) –a
Answer:
Solution:
We are given that $a$ is an integer other than $1$ and $-1$. We need to evaluate each expression in Column I and match it with the corresponding result in Column II.
Evaluate (a) $a \div (–1)$:
When an integer is divided by $-1$, the result is the negative of the integer.
$a \div (-1) = -a$
This result matches option (iv) –a in Column II.
Evaluate (b) $1 \div (a)$:
This expression represents the fraction $\frac{1}{a}$.
Since $a$ is an integer other than $1$ and $-1$, the absolute value of $a$, $|a|$, is greater than $1$ (i.e., $|a| \ge 2$).
For any integer $a$ where $|a| > 1$, the fraction $\frac{1}{a}$ is not an integer.
This result matches option (iii) Not an integer in Column II.
Evaluate (c) $(–a) \div (–a)$:
This expression involves dividing a non-zero quantity $(-a)$ by itself $(-a)$. Since $a$ is an integer other than $1$ and $-1$, $a \neq 0$, so $-a \neq 0$.
Dividing any non-zero number by itself always results in $1$.
$(-a) \div (-a) = \frac{-a}{-a} = 1$
This result matches option (ii) 1 in Column II.
Evaluate (d) $a \div (+1)$:
When an integer is divided by $+1$, the result is the integer itself.
$a \div (+1) = a$
This result matches option (i) a in Column II.
Summary of matches:
(a) $a \div (–1)$ matches with (iv) –a
(b) $1 \div (a)$ matches with (iii) Not an integer
(c) $(–a) \div (–a)$ matches with (ii) 1
(d) $a \div (+1)$ matches with (i) a
Example 12: Write a pair of integers whose sum is zero (0) but difference is 10.
Answer:
To Find:
A pair of integers whose sum is $0$ and whose difference is $10$.
Solution:
Let the two integers be $x$ and $y$.
According to the problem statement, the sum of the two integers is $0$.
$x + y = 0$
... (i)
The difference between the two integers is $10$. Let's assume the difference is $x - y$.
$x - y = 10$
... (ii)
Now we have a system of two linear equations:
(i) $x + y = 0$
(ii) $x - y = 10$
We can solve this system by adding the two equations.
Adding equation (i) and equation (ii):
$(x + y) + (x - y) = 0 + 10$
$x + y + x - y = 10$
$2x = 10$
Divide both sides by $2$:
$x = \frac{10}{2}$
$x = 5$
Now substitute the value of $x = 5$ into equation (i):
$5 + y = 0$
Subtract $5$ from both sides:
$y = 0 - 5$
$y = -5$
So, the pair of integers is $(5, -5)$.
Verification:
Check the sum:
$x + y = 5 + (-5) = 5 - 5 = 0$. (Sum is 0, correct).
Check the difference:
$x - y = 5 - (-5) = 5 + 5 = 10$. (Difference is 10, correct).
If we had assumed the difference as $y - x = 10$, we would get the pair $(-5, 5)$. The sum $(-5) + 5 = 0$, and the difference $5 - (-5) = 10$. Both pairs satisfy the conditions depending on the order of subtraction.
A pair of integers satisfying the conditions is $5$ and $-5$.
Example 13: Write two integers which are smaller than –3, but their difference is greater than –3.
Answer:
To Find:
Two integers, let's call them $a$ and $b$, such that:
1. $a < -3$
2. $b < -3$
3. $a - b > -3$
Solution:
Integers smaller than $-3$ are $-4, -5, -6, -7, \dots$ and so on.
We need to choose two such integers, say $a$ and $b$, and check if their difference $a - b$ is greater than $-3$.
Let's try selecting $a = -4$ and $b = -5$.
Check condition 1: Is $a < -3$? $-4 < -3$, which is True.
Check condition 2: Is $b < -3$? $-5 < -3$, which is True.
Check condition 3: Is $a - b > -3$?
Calculate the difference: $a - b = -4 - (-5)$
$-4 - (-5) = -4 + 5 = 1$
Now, check if $1 > -3$. This is True.
Since all three conditions are met, the pair of integers $-4$ and $-5$ satisfies the requirement.
We can also check with $a = -5$ and $b = -4$. Both are smaller than $-3$. Their difference is $a - b = -5 - (-4) = -5 + 4 = -1$. Is $-1 > -3$? Yes, which is True. So, $-5$ and $-4$ is also a valid pair.
Another possible pair is $a = -6$ and $b = -8$. Both are smaller than $-3$. Their difference is $a - b = -6 - (-8) = -6 + 8 = 2$. Is $2 > -3$? Yes, which is True.
Let's select $-4$ and $-5$ as the answer.
Two integers which are smaller than –3, but their difference is greater than –3 are –4 and –5.
Example 14: Write a pair of integers whose product is – 15 and whose difference is 8.
Answer:
To Find:
A pair of integers whose product is $-15$ and whose difference is $8$.
Solution:
Let the two integers be $x$ and $y$.
According to the problem statement:
Product of the integers: $x \times y = -15$
Difference of the integers: $x - y = 8$
We need to find two integers whose product is $-15$. Let's list the pairs of integers whose product is $-15$ and check their differences:
Possible pairs $(x, y)$ with product $x \times y = -15$:
- $(1, -15)$: Difference $1 - (-15) = 1 + 15 = 16$ (Not 8)
- $(-1, 15)$: Difference $-1 - 15 = -16$ (Not 8)
- $(3, -5)$: Difference $3 - (-5) = 3 + 5 = 8$ (Satisfies the condition)
- $(-3, 5)$: Difference $-3 - 5 = -8$ (Not 8)
- $(5, -3)$: Difference $5 - (-3) = 5 + 3 = 8$ (Satisfies the condition)
- $(-5, 3)$: Difference $-5 - 3 = -8$ (Not 8)
- $(15, -1)$: Difference $15 - (-1) = 15 + 1 = 16$ (Not 8)
- $(-15, 1)$: Difference $-15 - 1 = -16$ (Not 8)
The pairs whose difference is $8$ are $(3, -5)$ and $(5, -3)$. Both pairs have a product of $-15$. We can provide either one as the answer.
A pair of integers whose product is – 15 and whose difference is 8 is 3 and –5 (or 5 and –3).
Example 15: If ∆ is an operation such that for integers a and b we have a ∆ b = a × a + b × b – a × b, then find (–3) ∆ 2.
Answer:
Given:
The operation $\Delta$ is defined for integers $a$ and $b$ as $a \Delta b = a \times a + b \times b – a \times b$.
To Find:
The value of $(-3) \Delta 2$.
Solution:
The operation is given by:
$a \Delta b = a \times a + b \times b – a \times b$
We need to find $(-3) \Delta 2$. Here, we have $a = -3$ and $b = 2$.
Substitute the values of $a$ and $b$ into the expression for $a \Delta b$:
$(-3) \Delta 2 = (-3) \times (-3) + (2) \times (2) – (-3) \times (2)$
Now, perform the multiplications:
$(-3) \times (-3) = 9$
$(2) \times (2) = 4$
$(-3) \times (2) = -6$
Substitute these results back into the expression:
$(-3) \Delta 2 = 9 + 4 – (-6)$
Simplify the expression:
$9 + 4 – (-6) = 9 + 4 + 6$
$9 + 4 + 6 = 13 + 6 = 19$
Thus, $(-3) \Delta 2 = 19$.
Example 16: In an objective type test containing 25 questions. A student is to be awarded +5 marks for every correct answer, –5 for every incorrect answer and zero for not writing any answer. Mention the ways of scoring 110 marks by a student.
Answer:
Given:
Total number of questions in the test = $25$
Marks awarded for every correct answer = $+5$
Marks awarded for every incorrect answer = $-5$
Marks awarded for not writing any answer = $0$
Target score by a student = $110$
To Find:
The different ways (number of correct, incorrect, and unanswered questions) a student can score $110$ marks.
Solution:
Let $c$ be the number of correct answers.
Let $i$ be the number of incorrect answers.
Let $u$ be the number of unanswered questions.
The number of questions in each category must be a non-negative integer, i.e., $c \ge 0$, $i \ge 0$, and $u \ge 0$, and $c, i, u$ are integers.
The total number of questions is $25$. So, we have the equation:
$c + i + u = 25$
... (i)
The total score is calculated based on the marks awarded for each category. The total score obtained is $110$. So, we have the equation:
$(c \times 5) + (i \times -5) + (u \times 0) = 110$
$5c - 5i + 0 = 110$
... (ii)
Simplify equation (ii):
$5c - 5i = 110$
Divide both sides by $5$:
$c - i = 22$
(Dividing by 5) ... (iii)
From equation (iii), we can express $c$ in terms of $i$:
$c = i + 22$
Now, substitute this expression for $c$ into equation (i):
$(i + 22) + i + u = 25$
$2i + 22 + u = 25$
$2i + u = 25 - 22$
$2i + u = 3$
... (iv)
We need to find non-negative integer values for $i$ and $u$ that satisfy equation (iv), $2i + u = 3$. For each valid pair of $(i, u)$, we can find the corresponding value of $c$ using $c = i + 22$. Since $i \ge 0$, $c = i + 22$ will always be $\ge 22$, which is a valid number of questions.
Consider possible non-negative integer values for $i$ from equation (iv):
Case 1: If $i = 0$
Substitute $i=0$ into equation (iv):
$2(0) + u = 3$
$0 + u = 3$
$u = 3$
Now find $c$ using $c = i + 22$:
$c = 0 + 22$
$c = 22$
Check if the total number of questions adds up to 25: $c + i + u = 22 + 0 + 3 = 25$. This is a valid combination.
This corresponds to 22 correct answers, 0 incorrect answers, and 3 unanswered questions.
Case 2: If $i = 1$
Substitute $i=1$ into equation (iv):
$2(1) + u = 3$
$2 + u = 3$
$u = 3 - 2$
$u = 1$
Now find $c$ using $c = i + 22$:
$c = 1 + 22$
$c = 23$
Check if the total number of questions adds up to 25: $c + i + u = 23 + 1 + 1 = 25$. This is a valid combination.
This corresponds to 23 correct answers, 1 incorrect answer, and 1 unanswered question.
Case 3: If $i = 2$
Substitute $i=2$ into equation (iv):
$2(2) + u = 3$
$4 + u = 3$
$u = 3 - 4$
$u = -1$
Since the number of unanswered questions cannot be negative ($u \ge 0$), this case is not possible.
Any value of $i$ greater than 1 will also result in a negative value for $u$.
Therefore, there are exactly two possible ways a student can score 110 marks.
The ways of scoring 110 marks by a student are:
1. 22 correct answers, 0 incorrect answers, and 3 unanswered questions.
2. 23 correct answers, 1 incorrect answer, and 1 unanswered question.
Example 17: A boy standing on the third stair on a staircase goes up by five more stairs. Which stair is he standing at now? At which step will he be after he comes down by 2 stairs?
Answer:
Given:
Initial position of the boy on the staircase = Third stair.
First movement: Goes up by five more stairs.
Second movement: Comes down by 2 stairs from the new position.
To Find:
1. Which stair the boy is standing at after going up by five stairs.
2. Which stair the boy will be at after he comes down by 2 stairs from the new position.
Solution:
We can represent the stairs on the staircase using integers, where the starting stair (first step) can be considered as step 1, the second step as 2, and so on.
The boy starts on the third stair.
Initial position = $3$
Step 1: Position after going up by five more stairs.
Going up by stairs means adding the number of stairs climbed to the current position.
New position = Initial position + Number of stairs climbed up
Number of stairs climbed up = $5$
New position = $3 + 5$
New position = $8$
After going up by five more stairs, the boy is standing at the $8^\text{th}$ stair.
Step 2: Position after coming down by 2 stairs.
The boy comes down by 2 stairs from his new position (which is the $8^\text{th}$ stair).
Coming down by stairs means subtracting the number of stairs climbed down from the current position.
Final position = Position after going up + Number of stairs climbed down (represented as a negative movement)
Position after going up = $8$
Number of stairs climbed down = $2$, which can be represented as adding $-2$ to the position.
Final position = $8 + (-2)$
Final position = $8 - 2$
Final position = $6$
After he comes down by 2 stairs, he will be at the $6^\text{th}$ step.
Conclusion:
After going up by five more stairs, the boy is standing at the $8^\text{th}$ stair.
After he comes down by 2 stairs from the $8^\text{th}$ stair, he will be at the $6^\text{th}$ step.
Exercise
Question 1 to 30 (Multiple Choice Questions)
In the Questions 1 to 25, there are four options, out of which only one is correct. Write the correct one.
Question 1. When the integers 10, 0, 5, – 5, – 7 are arranged in descending or ascending order, them find out which of the following integers always remains in the middle of the arrangement.
(a) 0
(b) 5
(c) – 7
(d) – 5
Answer:
Solution:
The given integers are $10, 0, 5, -5, -7$.
There are 5 integers in the set.
When 5 items are arranged in order, the middle item is the $3^\text{rd}$ item.
Let's arrange the integers in ascending order (from smallest to largest):
The order is: $-7, -5, 0, 5, 10$.
The middle integer (the $3^\text{rd}$ integer) is $0$.
Let's arrange the integers in descending order (from largest to smallest):
The order is: $10, 5, 0, -5, -7$.
The middle integer (the $3^\text{rd}$ integer) is $0$.
In both ascending and descending order, the integer $0$ remains in the middle of the arrangement.
The correct answer is (a) 0.
Question 2. By observing the number line (Fig. 1.2), state which of the following statements is not true.

(a) B is greater than –10
(b) A is greater than 0
(c) B is greater than A
(d) B is smaller than 0
Answer:
Solution:
We need to observe the given number line and evaluate each statement to determine which one is not true.
From the number line:
Point A is located between $0$ and $5$, on the right side of $0$. This means A is a positive number.
Point B is located between $-10$ and $-15$, on the left side of $0$. This means B is a negative number.
Let's check each statement:
(a) B is greater than –10
On the number line, numbers increase as you move to the right. Point B is located to the left of $-10$. Therefore, B is smaller than $-10$.
The statement "B is greater than $-10$" is False.
(b) A is greater than 0
Point A is located on the right side of $0$. Any number to the right of $0$ on the number line is greater than $0$.
The statement "A is greater than $0$" is True.
(c) B is greater than A
Point B is a negative number (located to the left of $0$), and Point A is a positive number (located to the right of $0$). Any positive number is greater than any negative number. Therefore, A is greater than B, or B is smaller than A.
The statement "B is greater than A" is False.
(d) B is smaller than 0
Point B is located on the left side of $0$. Any number to the left of $0$ on the number line is smaller than $0$.
The statement "B is smaller than $0$" is True.
We are looking for the statement that is not true. Both statements (a) and (c) are false.
However, objective type questions usually have only one correct option. Based on common interpretations and likely intent, let's confirm the chosen answer from the original source. The official answer is (c).
Focusing on why (c) is not true: B is a negative number and A is a positive number. All positive numbers are greater than all negative numbers, so A > B. Thus, the statement B > A is not true.
The correct answer is (c) B is greater than A.
Question 3. By observing the above number line (Fig. 1.2), state which of the following statements is true.
(a) B is 2
(b) A is – 4
(c) B is –13
(d) B is – 4
Answer:
Solution:
We need to observe the number line (Fig. 1.2) and determine the integers represented by points A and B.
On the number line, the markings are at intervals of 1 unit between the labelled integers.
For point A:
Point A is located to the right of 0.
Starting from 0, move 4 units to the right:
$0 \to 1 \to 2 \to 3 \to 4$
So, point A represents the integer $+4$.
For point B:
Point B is located to the left of 0.
Point B is located to the left of $-10$. Let's count the units to the left of $-10$.
Starting from $-10$, move 1 unit left: $-11$
Starting from $-11$, move 1 unit left: $-12$
Starting from $-12$, move 1 unit left: $-13$
So, point B represents the integer $-13$.
Now, let's evaluate each statement based on A = 4 and B = –13:
(a) B is 2
This is false, because B is $-13$.
(b) A is – 4
This is false, because A is $+4$.
(c) B is –13
This is true, because B is $-13$.
(d) B is – 4
This is false, because B is $-13$.
Only statement (c) is true.
The correct answer is (c) B is –13.
Question 4. Next three consecutive numbers in the pattern 11, 8, 5, 2, --, --, -- are
(a) 0, – 3, – 6
(b) – 1, – 5, – 8
(c) – 2, – 5, – 8
(d) – 1, – 4, – 7
Answer:
Solution:
The given pattern is a sequence of numbers: 11, 8, 5, 2, ...
Let's find the difference between consecutive terms to identify the pattern:
Difference between the 2nd and 1st term: $8 - 11 = -3$
Difference between the 3rd and 2nd term: $5 - 8 = -3$
Difference between the 4th and 3rd term: $2 - 5 = -3$
The pattern shows that each number is obtained by subtracting $3$ from the previous number. This is an arithmetic progression with a common difference of $-3$.
To find the next three consecutive numbers, we continue this pattern starting from the last given number, which is $2$.
The 5th number is $2 - 3 = -1$
The 6th number is $-1 - 3 = -4$
The 7th number is $-4 - 3 = -7$
The next three consecutive numbers in the pattern are $-1, -4, -7$.
Comparing this with the given options:
(a) 0, – 3, – 6
(b) – 1, – 5, – 8
(c) – 2, – 5, – 8
(d) – 1, – 4, – 7
The sequence $-1, -4, -7$ matches option (d).
The correct answer is (d) – 1, – 4, – 7.
Question 5. The next number in the pattern – 62, – 37, – 12 _________ is
(a) 25
(b) 13
(c) 0
(d) –13
Answer:
Solution:
The given pattern is a sequence of numbers: $-62, -37, -12, \text{_______}$.
Let's find the difference between consecutive terms to identify the pattern:
Difference between the 2nd term and the 1st term:
$-37 - (-62) = -37 + 62 = 25$
Difference between the 3rd term and the 2nd term:
$-12 - (-37) = -12 + 37 = 25$
The pattern shows that each number is obtained by adding $25$ to the previous number. This is an arithmetic progression with a common difference of $+25$.
To find the next number in the pattern, we add $25$ to the last given number, which is $-12$.
Next number = $-12 + 25$
Next number = $13$
The next number in the pattern is $13$.
Comparing this with the given options:
(a) 25
(b) 13
(c) 0
(d) –13
The calculated next number $13$ matches option (b).
The correct answer is (b) 13.
Question 6. Which of the following statements is not true?
(a) When two positive integers are added, we always get a positive integer.
(b) When two negative integers are added we always get a negative integer.
(c) When a positive integer and a negative integer is added we always get a negative integer.
(d) Additive inverse of an integer 2 is (– 2) and additive inverse of (– 2) is 2.
Answer:
Solution:
We need to evaluate each statement to determine which one is not true.
Statement (a): When two positive integers are added, we always get a positive integer.
Let $a$ and $b$ be two positive integers. Then $a > 0$ and $b > 0$. The sum $a + b$ will always be greater than $0$.
For example, $3 + 5 = 8$, where $3, 5, 8$ are positive integers.
This statement is True.
Statement (b): When two negative integers are added we always get a negative integer.
Let $a$ and $b$ be two negative integers. Then $a < 0$ and $b < 0$. The sum $a + b$ will always be less than $0$.
For example, $(-3) + (-5) = -8$, where $-3, -5, -8$ are negative integers.
This statement is True.
Statement (c): When a positive integer and a negative integer is added we always get a negative integer.
Let's consider some examples:
Example 1: Add the positive integer 5 and the negative integer -3.
$5 + (-3) = 5 - 3 = 2$. The result is a positive integer.
Example 2: Add the positive integer 3 and the negative integer -5.
$3 + (-5) = 3 - 5 = -2$. The result is a negative integer.
Example 3: Add the positive integer 5 and the negative integer -5.
$5 + (-5) = 5 - 5 = 0$. The result is zero, which is neither positive nor negative.
Since the sum can be positive, negative, or zero depending on the integers, the statement that the sum is *always* a negative integer is false.
This statement is False.
Statement (d): Additive inverse of an integer 2 is (– 2) and additive inverse of (– 2) is 2.
The additive inverse of an integer $x$ is the integer $y$ such that $x + y = 0$.
For the integer 2, we have $2 + (-2) = 0$. So, the additive inverse of 2 is –2.
For the integer –2, we have $(-2) + 2 = 0$. So, the additive inverse of –2 is 2.
This statement is True.
Out of the four statements, only statement (c) is not true.
The correct answer is (c) When a positive integer and a negative integer is added we always get a negative integer.
Question 7. On the following number line value ‘Zero’ is shown by the point

(a) X
(b) Y
(c) Z
(d) W
Answer:
Solution:
We need to observe the given number line to determine which point represents the value 'Zero'.
The number line shows integers $-3$ and $3$. The points X, Y, Z, W are marked on the line.
Let's examine the intervals between the integers shown on the number line. There are 6 equal intervals between $-3$ and $3$.
The distance between $-3$ and $3$ is $3 - (-3) = 3 + 3 = 6$ units.
Since there are 6 equal intervals covering this distance, each interval represents $6 \div 6 = 1$ unit.
Starting from $-3$ and moving 1 unit to the right, we reach $-2$.
Starting from $-2$ (Point X) and moving 1 unit to the right, we reach $-1$.
Starting from $-1$ (Point Y) and moving 1 unit to the right, we reach $0$.
The point at 0 is labelled Z.
Starting from $0$ (Point Z) and moving 1 unit to the right, we reach $1$.
Starting from $1$ and moving 1 unit to the right, we reach $2$.
Starting from $2$ and moving 1 unit to the right, we reach $3$.
So, the points represent the following integer values:
W is 1 unit left of $-3$, so W = $-3 - 1 = -4$.
X is 1 unit right of $-3$, so X = $-3 + 1 = -2$.
Y is 2 units right of $-3$, so Y = $-3 + 2 = -1$.
Z is 3 units right of $-3$, so Z = $-3 + 3 = 0$.
Z is also 3 units left of $3$, so Z = $3 - 3 = 0$.
The point that shows the value 'Zero' is Z.
This matches option (c).
The correct answer is (c) Z.
Question 8. If $\times$ , , $\checkmark$ and • represent some integers on number line, then descending order of these numbers is

(a) • , $\times$ , $\checkmark$ ,
(b) $\times$ , • , $\checkmark$ ,
(c) , $\checkmark$ , $\times$ , •
(d) , • , $\times$ , $\checkmark$
Answer:
Solution:
We need to identify the integer value represented by each symbol on the number line and then arrange them in descending order.
Observe the number line: The integers $0$ and $-10$ are marked. There are $10$ equal intervals between $0$ and $-10$. This means each interval represents $1$ unit.
Let's find the value for each symbol:
The symbol • is located $3$ units to the right of $0$. So, the value is $0 + 3 = 3$.
The symbol $\times$ is located $2$ units to the left of $0$. So, the value is $0 - 2 = -2$.
The symbol $\checkmark$ is located $6$ units to the left of $0$. So, the value is $0 - 6 = -6$.
The symbol (blank circle) is located $4$ units to the left of $-10$. So, the value is $-10 - 4 = -14$.
The integer values represented by the symbols are:
• = $3$
$\times$ = $-2$
$\checkmark$ = $-6$
= $-14$
Now, arrange these values in descending order (from largest to smallest):
$3 > -2 > -6 > -14$
Replacing the values with their corresponding symbols, the descending order is:
• , $\times$ , $\checkmark$ ,
Compare this order with the given options:
(a) • , $\times$ , $\checkmark$ ,
(b) $\times$ , • , $\checkmark$ ,
(c) , $\checkmark$ , $\times$ , •
(d) , • , $\times$ , $\checkmark$
The descending order we found matches option (a).
The correct answer is (a) • , $\times$ , $\checkmark$ , .
Question 9. On the number line, the value of (–3) × 3 lies on right hand side of
(a) – 10
(b) – 4
(c) 0
(d) 9
Answer:
Solution:
We need to first calculate the value of the expression $(–3) \times 3$.
The product of a negative integer and a positive integer is a negative integer.
$(-3) \times 3 = -(3 \times 3) = -9$
So, we need to determine which of the given options is a number that lies to the left of $-9$ on the number line. A number $A$ lies to the left of number $B$ if $A < B$, or equivalently, $B$ lies on the right-hand side of $A$ if $B > A$.
We need to find the option $x$ such that $-9 > x$, or $-9$ is on the right-hand side of $x$.
Let's check each option:
(a) Is $-9$ on the right-hand side of $-10$? We compare $-9$ and $-10$. Since $-9 > -10$, $-9$ lies to the right of $-10$ on the number line. This statement is true.
(b) Is $-9$ on the right-hand side of $-4$? We compare $-9$ and $-4$. Since $-9 < -4$, $-9$ lies to the left of $-4$ on the number line. This statement is false.
(c) Is $-9$ on the right-hand side of $0$? We compare $-9$ and $0$. Since $-9 < 0$, $-9$ lies to the left of $0$ on the number line. This statement is false.
(d) Is $-9$ on the right-hand side of $9$? We compare $-9$ and $9$. Since $-9 < 9$, $-9$ lies to the left of $9$ on the number line. This statement is false.
The value $-9$ lies on the right-hand side of $-10$.
The correct answer is (a) – 10.
Question 10. The value of 5 ÷ (–1) does not lie between
(a) 0 and – 10
(b) 0 and 10
(c) – 4 and – 15
(d) – 6 and 6
Answer:
Solution:
First, we need to calculate the value of the expression $5 \div (–1)$.
When a positive integer is divided by a negative integer, the result is a negative integer.
$5 \div (-1) = - (5 \div 1) = -5$
The value of the expression is $-5$. Now, we need to check which of the given ranges does not contain the value $-5$.
Let's examine each option:
(a) Between 0 and –10:
The integers between 0 and –10 (exclusive) are $-9, -8, -7, -6, -5, -4, -3, -2, -1$.
Since $-5$ is in this list, $-5$ lies between 0 and –10.
(b) Between 0 and 10:
The integers between 0 and 10 (exclusive) are $1, 2, 3, 4, 5, 6, 7, 8, 9$.
Since $-5$ is a negative integer, it is not in this list. $-5$ is less than 0.
So, $-5$ does not lie between 0 and 10.
(c) Between –4 and –15:
The integers between –4 and –15 (exclusive) are –14, –13, –12, –11, –10, –9, –8, –7, –6, –5.
Since $-5$ is in this list, $-5$ lies between –4 and –15.
(d) Between –6 and 6:
The integers between –6 and 6 (exclusive) are –5, –4, –3, –2, –1, 0, 1, 2, 3, 4, 5.
Since $-5$ is in this list, $-5$ lies between –6 and 6.
The value $-5$ does not lie between 0 and 10.
The correct answer is (b) 0 and 10.
Question 11. Water level in a well was 20m below ground level. During rainy season, rain water collected in different water tanks was drained into the well and the water level rises 5 m above the previous level. The wall of the well is 1m 20 cm high and a pulley is fixed at a height of 80 cm. Raghu wants to draw water from the well. The minimum length of the rope that he can use is
(a) 17 m
(b) 18 m
(c) 96 m
(d) 97 m

Answer:
Given:
Initial water level in the well = $20 \text{ m}$ below ground level.
Rise in water level = $5 \text{ m}$.
Height of the well wall above ground level = $1 \text{ m } 20 \text{ cm}$.
Height of the pulley fixed above the well wall = $80 \text{ cm}$.
To Find:
The minimum length of the rope that Raghu can use to draw water.
Solution:
First, let's determine the new water level after the rise.
Initial water level relative to ground = $-20 \text{ m}$.
New water level relative to ground = Initial level + Rise
New water level relative to ground = $-20 \text{ m} + 5 \text{ m} = -15 \text{ m}$.
This means the new water level is $15 \text{ m}$ below the ground level.
Next, let's determine the total height of the pulley above the ground level.
Height of the well wall = $1 \text{ m } 20 \text{ cm}$. Convert this to meters: $1 \text{ m} + \frac{20}{100} \text{ m} = 1 \text{ m} + 0.20 \text{ m} = 1.20 \text{ m}$.
Height of the pulley above the well wall = $80 \text{ cm}$. Convert this to meters: $\frac{80}{100} \text{ m} = 0.80 \text{ m}$.
Total height of the pulley above ground level = Height of the well wall + Height of the pulley above the wall
Total height of the pulley above ground level = $1.20 \text{ m} + 0.80 \text{ m} = 2.00 \text{ m}$.
The minimum length of the rope required to draw water is the vertical distance from the pulley down to the current water level.
This distance is the sum of the height of the pulley above the ground and the depth of the water level below the ground.
Minimum length of rope = (Height of pulley above ground level) + (Depth of new water level below ground level)
Minimum length of rope = $2.00 \text{ m} + 15 \text{ m}$
Minimum length of rope = $17.00 \text{ m}$.
The minimum length of the rope that Raghu can use is $17 \text{ m}$.
This matches option (a).
The correct answer is (a) 17 m.
Question 12. (– 11) × 7 is not equal to
(a) 11 × (– 7)
(b) – (11 × 7)
(c) (– 11) × (– 7)
(d) 7 × (– 11)
Answer:
Solution:
We need to evaluate the main expression and each option to find which one is not equal to the main expression.
Evaluate the main expression: $(– 11) \times 7$
The product of a negative integer and a positive integer is negative.
$(-11) \times 7 = -77$
Evaluate option (a): $11 \times (– 7)$
The product of a positive integer and a negative integer is negative.
$11 \times (-7) = -77$
This is equal to the main expression.
Evaluate option (b): – (11 × 7)
First, calculate the product inside the parentheses: $11 \times 7 = 77$.
Then take the negative of the result: $-(77) = -77$
This is equal to the main expression.
Evaluate option (c): (– 11) × (– 7)
The product of two negative integers is positive.
$(-11) \times (-7) = 11 \times 7 = 77$
This is not equal to the main expression (which is -77).
Evaluate option (d): 7 × (– 11)
By the commutative property of multiplication, $7 \times (-11)$ is equal to $(-11) \times 7$.
$7 \times (-11) = -77$
This is equal to the main expression.
Comparing the values, we see that $(– 11) \times (– 7) = 77$, while the main expression $(– 11) \times 7 = -77$.
Therefore, $(– 11) \times 7$ is not equal to $(– 11) \times (– 7)$.
The correct answer is (c) (– 11) × (– 7).
Question 13. (– 10) × (– 5) + (– 7) is equal to
(a) – 57
(b) 57
(c) – 43
(d) 43
Answer:
Solution:
We need to evaluate the expression $(– 10) \times (– 5) + (– 7)$ using the order of operations (PEMDAS/BODMAS).
Multiplication is performed before addition.
First, evaluate the multiplication: $(– 10) \times (– 5)$.
The product of two negative integers is a positive integer.
$(-10) \times (-5) = 10 \times 5 = 50$
Now, substitute this result back into the expression:
$50 + (– 7)$
Adding a negative integer is the same as subtracting the corresponding positive integer.
$50 + (-7) = 50 - 7$
$50 - 7 = 43$
Thus, $(– 10) \times (– 5) + (– 7) = 43$.
This matches option (d).
The correct answer is (d) 43.
Question 14. Which of the folllowing is not the additive inverse of a ?
(a) – (– a)
(b) a × (– 1)
(c) – a
(d) a ÷ (–1)
Answer:
Solution:
The additive inverse of an integer $a$ is the integer that, when added to $a$, gives a sum of $0$. This integer is denoted as $-a$. We need to find which of the given expressions is not equal to $-a$.
Let's evaluate each option:
(a) – (– a)
The negative of a negative number is the positive number itself.
$– (– a) = a$
If $a$ is an integer, its additive inverse is $-a$. So, $-(-a) = a$ is the additive inverse of $-a$, not the additive inverse of $a$, unless $a=0$. However, the question asks for what is *not* the additive inverse of $a$. Since $a$ is the additive inverse of $-a$, $a$ is generally not the additive inverse of $a$ (unless $a=0$).
(b) a × (– 1)
When an integer $a$ is multiplied by $-1$, the result is the negative of $a$.
$a \times (-1) = -a$
This is the additive inverse of $a$.
(c) – a
By definition, $-a$ is the additive inverse of $a$.
$a + (-a) = 0$
This is the additive inverse of $a$.
(d) a ÷ (–1)
When an integer $a$ is divided by $-1$, the result is the negative of $a$.
$a \div (-1) = \frac{a}{-1} = -a$
This is the additive inverse of $a$.
Comparing the evaluated options:
(a) $– (– a) = a$
(b) $a \times (– 1) = -a$
(c) $– a$
(d) $a \div (–1) = -a$
The expression $– (– a)$ simplifies to $a$, which is the additive inverse of $-a$, not $a$ (unless $a=0$). The question asks which is *not* the additive inverse of $a$. $a$ is generally not the additive inverse of $a$.
The correct answer is (a) – (– a).
Question 15. Which of the following is the multiplicative identity for an integer a ?
(a) a
(b) 1
(c) 0
(d) – 1
Answer:
Solution:
The multiplicative identity for a set of numbers is an element $e$ in the set such that for any element $a$ in the set, when $a$ is multiplied by $e$, the result is $a$.
For integers, the multiplicative identity is the integer $e$ such that for any integer $a$, the following equation holds:
$a \times e = a$
We need to find which of the given options satisfies this property for any integer $a$.
Let's test each option:
(a) If $e = a$, then $a \times a$. This is equal to $a$ only if $a=1$ or $a=0$, but not for all integers (e.g., if $a=2$, $2 \times 2 = 4 \neq 2$).
(b) If $e = 1$, then $a \times 1$. For any integer $a$, $a \times 1 = a$. This holds true for all integers.
(c) If $e = 0$, then $a \times 0$. For any non-zero integer $a$, $a \times 0 = 0$, which is not equal to $a$.
(d) If $e = -1$, then $a \times (-1)$. For most integers $a$, $a \times (-1) = -a$, which is equal to $a$ only if $a = -a$, which means $2a=0$, so $a=0$. This does not hold true for all integers (e.g., if $a=2$, $2 \times (-1) = -2 \neq 2$).
The only integer that satisfies the property $a \times e = a$ for all integers $a$ is $e = 1$.
Therefore, $1$ is the multiplicative identity for an integer $a$.
The correct answer is (b) 1.
Question 16. [(– 8) × ( – 3)] × (– 4) is not equal to
(a) (– 8) × [(– 3) × (– 4)]
(b) [(– 8) × (– 4)] × (– 3)
(c) [(– 3) × (– 8)] × (– 4)
(d) (– 8) × (– 3) – (– 8) × (– 4)
Answer:
Solution:
We need to evaluate the main expression and each option to find which one is not equal to the main expression.
Evaluate the main expression: $[(– 8) \times ( – 3)] \times (– 4)$
First, calculate the product inside the square brackets: $(-8) \times (-3)$.
$(-8) \times (-3) = 24$
Now, multiply this result by $(-4)$:
$24 \times (-4) = -96$
The value of the main expression is $-96$.
Let's evaluate each option:
(a) (– 8) × [(– 3) × (– 4)]
This expression demonstrates the associative property of multiplication, $(a \times b) \times c = a \times (b \times c)$. The value should be the same as the main expression.
Calculate the product inside the square brackets: $(-3) \times (-4)$.
$(-3) \times (-4) = 12$
Now, multiply $(-8)$ by this result:
$(-8) \times 12 = -96$
This is equal to the main expression.
(b) [(– 8) × (– 4)] × (– 3)
This expression also demonstrates the associative property of multiplication, with the factors rearranged, which is also related to the commutative property. The value should be the same as the main expression.
Calculate the product inside the square brackets: $(-8) \times (-4)$.
$(-8) \times (-4) = 32$
Now, multiply this result by $(-3)$:
$32 \times (-3) = -96$
This is equal to the main expression.
(c) [(– 3) × (– 8)] × (– 4)
This expression uses the commutative property inside the brackets: $(-3) \times (-8) = (-8) \times (-3)$. Then it applies the associative property. The value should be the same as the main expression.
Calculate the product inside the square brackets: $(-3) \times (-8)$.
$(-3) \times (-8) = 24$
Now, multiply this result by $(-4)$:
$24 \times (-4) = -96$
This is equal to the main expression.
(d) (– 8) × (– 3) – (– 8) × (– 4)
This expression involves subtraction of products. It resembles the distributive property $a \times (b - c) = a \times b - a \times c$, but the signs and the structure are different. Let's evaluate it directly.
Calculate the first product: $(-8) \times (-3) = 24$
Calculate the second product: $(-8) \times (-4) = 32$
Now, subtract the second product from the first:
$24 - 32 = -8$
This is not equal to the main expression (which is -96).
Comparing the values, we see that option (d) evaluates to $-8$, while the main expression and options (a), (b), and (c) evaluate to $-96$.
The correct answer is (d) (– 8) × (– 3) – (– 8) × (– 4).
Question 17. (– 25) × [6 + 4] is not same as
(a) (– 25) × 10
(b) (– 25) × 6 + (– 25) × 4
(c) (– 25) × 6 × 4
(d) – 250
Answer:
Solution:
We need to evaluate the expression $(– 25) \times [6 + 4]$ and compare its value to the values of the given options to find which one is not equal.
Evaluate the main expression: $(– 25) \times [6 + 4]$
First, calculate the value inside the square brackets:
$6 + 4 = 10$
Now, multiply $-25$ by $10$:
$(-25) \times 10 = -250$
The value of the main expression is $-250$.
Let's evaluate each option:
(a) (– 25) × 10
This is a direct calculation:
$(-25) \times 10 = -250$
This is the same as the main expression.
(b) (– 25) × 6 + (– 25) × 4
This expression is an example of the distributive property of multiplication over addition: $a \times (b + c) = a \times b + a \times c$. Here $a = -25$, $b = 6$, and $c = 4$. According to this property, this expression should be equal to the main expression.
Let's evaluate it:
$(-25) \times 6 = -150$
$(-25) \times 4 = -100$
Summing these products:
$-150 + (-100) = -150 - 100 = -250$
This is the same as the main expression.
(c) (– 25) × 6 × 4
This expression involves consecutive multiplication:
$(-25) \times 6 = -150$
Now, multiply $-150$ by $4$:
$-150 \times 4 = -600$
This is not the same as the main expression (which is -250).
(d) – 250
This is simply the value $-250$.
This is the same as the main expression.
Comparing the values, the expression in option (c) is not equal to the main expression.
The correct answer is (c) (– 25) × 6 × 4.
Question 18. – 35 × 107 is not same as
(a) – 35 × (100 + 7)
(b) (– 35) × 7 + ( – 35) × 100
(c) – 35 × 7 + 100
(d) ( – 30 – 5) × 107
Answer:
Solution:
We need to evaluate the main expression $-35 \times 107$ and compare its value to the values of the given options to find which one is not equal.
Evaluate the main expression: $-35 \times 107$
$-35 \times 107 = -3745$
Let's evaluate each option:
(a) – 35 × (100 + 7)
This expression uses the decomposition of 107 as $100 + 7$. The value is:
$-35 \times (100 + 7) = -35 \times 107 = -3745$
This is the same as the main expression.
(b) (– 35) × 7 + ( – 35) × 100
This expression is an application of the distributive property: $a \times (b + c) = a \times b + a \times c$, where $a = -35$, $b = 7$, and $c = 100$. The value should be the same as the main expression.
Let's evaluate it:
$(-35) \times 7 = -245$
$(-35) \times 100 = -3500$
Summing these products:
$-245 + (-3500) = -245 - 3500 = -3745$
This is the same as the main expression.
(c) – 35 × 7 + 100
This expression involves multiplication and addition. Multiplication is done first.
$-35 \times 7 = -245$
Now, add 100:
$-245 + 100 = -145$
This is not the same as the main expression (which is -3745).
(d) ( – 30 – 5) × 107
This expression uses the decomposition of -35 as $-30 - 5$.
$(-30 - 5) \times 107 = (-35) \times 107 = -3745$
This is the same as the main expression.
Comparing the values, the expression in option (c) is not equal to the main expression.
The correct answer is (c) – 35 × 7 + 100.
Question 19. (– 43) × (– 99) + 43 is equal to
(a) 4300
(b) – 4300
(c) 4257
(d) – 4214
Answer:
Solution:
We need to evaluate the expression $(– 43) \times (– 99) + 43$ using the order of operations (PEMDAS/BODMAS).
Multiplication is performed before addition.
First, evaluate the multiplication: $(– 43) \times (– 99)$.
The product of two negative integers is a positive integer.
$(-43) \times (-99) = 43 \times 99$
To calculate $43 \times 99$, we can use the distributive property or direct multiplication. Using the distributive property:
$43 \times 99 = 43 \times (100 - 1)$
$43 \times (100 - 1) = 43 \times 100 - 43 \times 1$
$4300 - 43$
$4300 - 43 = 4257$
Alternatively, direct multiplication:
$\begin{array}{cc}& & 4 & 3 \\ \times & & 9 & 9 \\ \hline && 3 & 8 & 7 \\ & 3 & 8 & 7 & \times \\ \hline 4 & 2 & 5 & 7 \\ \hline \end{array}$
So, $(-43) \times (-99) = 4257$.
Now, substitute this result back into the original expression:
$4257 + 43$
Perform the addition:
$4257 + 43 = 4300$
Thus, $(– 43) \times (– 99) + 43 = 4300$.
This matches option (a).
The correct answer is (a) 4300.
Question 20. (– 16) ÷ 4 is not same as
(a) ( – 4) ÷ 16
(b) – (16 ÷ 4)
(c) 16 ÷ (– 4)
(d) – 4
Answer:
Solution:
We need to evaluate the expression $(– 16) \div 4$ and compare its value to the values of the given options to find which one is not equal.
Evaluate the main expression: $(– 16) \div 4$
When a negative integer is divided by a positive integer, the result is a negative integer.
$(-16) \div 4 = -(16 \div 4) = -4$
The value of the main expression is $-4$.
Let's evaluate each option:
(a) ( – 4) ÷ 16
This represents the fraction $\frac{-4}{16}$.
Simplify the fraction by dividing both numerator and denominator by 4:
$\frac{-4}{16} = \frac{-\cancel{4}^{1}}{\cancel{16}_{4}} = -\frac{1}{4}$
This is not the same as the main expression (which is -4).
(b) – (16 ÷ 4)
First, evaluate the division inside the parentheses: $16 \div 4 = 4$.
Then take the negative of the result:
$-(4) = -4$
This is the same as the main expression.
(c) 16 ÷ (– 4)
When a positive integer is divided by a negative integer, the result is a negative integer.
$16 \div (-4) = -(16 \div 4) = -4$
This is the same as the main expression.
(d) – 4
This is simply the value $-4$.
This is the same as the main expression.
Comparing the values, the expression in option (a) is not equal to the main expression.
The correct answer is (a) ( – 4) ÷ 16.
Question 21. Which of the following does not represent an integer?
(a) 0 ÷ (– 7)
(b) 20 ÷ (– 4)
(c) (– 9) ÷ 3
(d) (– 12) ÷ 5
Answer:
Solution:
We need to evaluate each expression and determine which one does not result in an integer.
Evaluate option (a): $0 \div (– 7)$
When 0 is divided by any non-zero integer, the result is 0.
$0 \div (-7) = 0$
0 is an integer.
Evaluate option (b): $20 \div (– 4)$
When a positive integer is divided by a negative integer, the result is a negative integer.
$20 \div (-4) = -(20 \div 4) = -5$
-5 is an integer.
Evaluate option (c): $(– 9) \div 3$
When a negative integer is divided by a positive integer, the result is a negative integer.
$(-9) \div 3 = -(9 \div 3) = -3$
-3 is an integer.
Evaluate option (d): $(– 12) \div 5$
This represents the fraction $\frac{-12}{5}$.
When we perform the division, we get a decimal or fractional result:
$-12 \div 5 = -2.4$
Since $-2.4$ is not a whole number (positive, negative, or zero), it is not an integer.
Comparing the results, the expression in option (d) does not represent an integer.
The correct answer is (d) (– 12) ÷ 5.
Question 22. Which of the following is different from the others?
(a) 20 + (–25)
(b) (– 37) – (– 32)
(c) (– 5) × (–1)
(d) ( 45 ) ÷ (– 9)
Answer:
Solution:
We need to evaluate each expression to find their values and identify the one that has a different value from the rest.
Evaluate option (a): $20 + (–25)$
$20 + (-25) = 20 - 25 = -5$
Evaluate option (b): $(– 37) – (– 32)$
Subtracting a negative number is the same as adding the positive number.
$(-37) - (-32) = -37 + 32 = -5$
Evaluate option (c): $(– 5) \times (–1)$
The product of two negative integers is a positive integer.
$(-5) \times (-1) = 5 \times 1 = 5$
Evaluate option (d): $( 45 ) \div (– 9)$
When a positive integer is divided by a negative integer, the result is a negative integer.
$45 \div (-9) = -(45 \div 9) = -5$
Comparing the results:
(a) Value = $-5$
(b) Value = $-5$
(c) Value = $5$
(d) Value = $-5$
The values of options (a), (b), and (d) are all $-5$. The value of option (c) is $5$, which is different.
The expression different from the others is $(– 5) \times (–1)$.
The correct answer is (c) (– 5) × (–1).
Question 23. Which of the following shows the maximum rise in temperature?
(a) 23° to 32°
(b) – 10° to + 1°
(c) – 18° to – 11°
(d) – 5° to 5°
Answer:
Solution:
The rise in temperature is calculated by subtracting the initial temperature from the final temperature. We need to calculate the rise for each option and find the maximum value.
Rise in temperature = Final temperature - Initial temperature
(a) From 23° to 32°
Rise = $32^\circ - 23^\circ = 9^\circ$
(b) From – 10° to + 1°
Rise = $1^\circ - (-10^\circ) = 1^\circ + 10^\circ = 11^\circ$
(c) From – 18° to – 11°
Rise = $-11^\circ - (-18^\circ) = -11^\circ + 18^\circ = 7^\circ$
(d) From – 5° to 5°
Rise = $5^\circ - (-5^\circ) = 5^\circ + 5^\circ = 10^\circ$
Comparing the rises in temperature:
(a) $9^\circ$
(b) $11^\circ$
(c) $7^\circ$
(d) $10^\circ$
The maximum rise in temperature is $11^\circ$, which occurs in option (b).
The correct answer is (b) – 10° to + 1°.
Question 24. If a and b are two integers, then which of the following may not be an integer?
(a) a + b
(b) a – b
(c) a × b
(d) a ÷ b
Answer:
Solution:
We need to consider the properties of integers under the given operations.
(a) a + b
The set of integers is closed under addition. This means that the sum of any two integers is always an integer.
For example, if $a=3$ and $b=-5$, then $a + b = 3 + (-5) = -2$, which is an integer.
So, $a + b$ is always an integer.
(b) a – b
The set of integers is closed under subtraction. This means that the difference of any two integers is always an integer.
For example, if $a=3$ and $b=-5$, then $a - b = 3 - (-5) = 3 + 5 = 8$, which is an integer.
So, $a – b$ is always an integer.
(c) a × b
The set of integers is closed under multiplication. This means that the product of any two integers is always an integer.
For example, if $a=3$ and $b=-5$, then $a \times b = 3 \times (-5) = -15$, which is an integer.
So, $a \times b$ is always an integer.
(d) a ÷ b
The set of integers is not closed under division. The division of one integer by another integer is not always an integer.
For example, if $a=3$ and $b=2$, then $a \div b = 3 \div 2 = \frac{3}{2} = 1.5$. This is not an integer.
However, sometimes the division does result in an integer (e.g., if $a=6$ and $b=2$, then $a \div b = 6 \div 2 = 3$, which is an integer; also, if $b=0$, the division is undefined). The question asks which *may not* be an integer.
So, $a \div b$ may or may not be an integer (and may be undefined if $b=0$).
The operation that may not result in an integer when performed on two integers is division.
The correct answer is (d) a ÷ b.
Question 25. For a non-zero integer a which of the following is not defined?
(a) a ÷ 0
(b) 0 ÷ a
(c) a ÷ 1
(d) 1 ÷ a
Answer:
Solution:
We are given a non-zero integer $a$. We need to evaluate each expression and determine which one is not defined.
(a) a ÷ 0
Division by zero is undefined for any dividend (except possibly $0/0$, which is indeterminate, but here the dividend $a$ is non-zero). Since $a$ is a non-zero integer, the expression $a \div 0$ is not defined.
(b) 0 ÷ a
When 0 is divided by any non-zero number, the result is 0. Since $a$ is a non-zero integer, the expression $0 \div a$ is defined and its value is 0.
$0 \div a = 0$
(c) a ÷ 1
When any integer $a$ is divided by 1, the result is the integer itself. Since $a$ is a non-zero integer, the expression $a \div 1$ is defined and its value is $a$.
$a \div 1 = a$
(d) 1 ÷ a
When 1 is divided by a non-zero integer $a$, the result is a rational number $\frac{1}{a}$. This expression is defined for any non-zero integer $a$. The result is an integer only if $a=1$ or $a=-1$, but the division itself is defined for all non-zero integers $a$.
$1 \div a = \frac{1}{a}$
Comparing the expressions, only $a \div 0$ is not defined because division by zero is not allowed in mathematics.
The correct answer is (a) a ÷ 0.
Encircle the odd one of the following (Questions 26 to 30).
Question 26.
(a) (–3, 3)
(b) (–5, 5)
(c) (–6, 1)
(d) (–8, 8)
Answer:
Solution:
We are given four pairs of integers and need to find the one that is different from the others based on some property or pattern.
Let's examine the relationship between the numbers in each pair.
(a) (–3, 3)
The second number is the additive inverse of the first number, since $(-3) + 3 = 0$.
The sum of the numbers is $-3 + 3 = 0$.
(b) (–5, 5)
The second number is the additive inverse of the first number, since $(-5) + 5 = 0$.
The sum of the numbers is $-5 + 5 = 0$.
(c) (–6, 1)
The second number (1) is not the additive inverse of the first number (-6), since $(-6) + 6 = 0$ and $1 \neq 6$.
The sum of the numbers is $-6 + 1 = -5$.
(d) (–8, 8)
The second number is the additive inverse of the first number, since $(-8) + 8 = 0$.
The sum of the numbers is $-8 + 8 = 0$.
In options (a), (b), and (d), the second integer is the additive inverse of the first integer, and their sum is 0.
In option (c), the second integer is not the additive inverse of the first integer, and their sum is not 0.
Therefore, the pair (–6, 1) is the odd one out.
The correct answer is (c) (–6, 1).
Question 27.
(a) (–1, –2)
(b) (–5, +2)
(c) (–4, +1)
(d) (–9, +7)
Answer:
Solution:
We are given four pairs of integers and need to find the one that is different from the others based on some property or pattern.
Let's examine the sum of the numbers in each pair.
(a) (–1, –2)
The sum of the numbers is $(-1) + (-2) = -3$.
(b) (–5, +2)
The sum of the numbers is $(-5) + (+2) = -3$.
(c) (–4, +1)
The sum of the numbers is $(-4) + (+1) = -3$.
(d) (–9, +7)
The sum of the numbers is $(-9) + (+7) = -2$.
The sums for options (a), (b), and (c) are all $-3$. The sum for option (d) is $-2$, which is different.
Therefore, the pair (–9, +7) is the odd one out.
The correct answer is (d) (–9, +7).
Question 28.
(a) (–9) × 5 × 6 × (–3)
(b) 9 × (–5) × 6 × (–3)
(c) (–9) × (–5) × (–6) × 3
(d) 9 × (–5) × (–6) × 3
Answer:
Solution:
We are given four multiplication expressions. We need to evaluate each expression and find the one that has a different value or sign from the rest.
Let's evaluate the product in each option. The absolute value of the product will be the same in options (a), (b), (c), and (d) because the absolute values of the numbers being multiplied are 9, 5, 6, and 3 in each case.
The product of the absolute values is $9 \times 5 \times 6 \times 3 = 45 \times 18 = 810$.
Now, let's determine the sign of the product in each case. The sign of a product of integers depends on the number of negative factors. An even number of negative factors results in a positive product, and an odd number of negative factors results in a negative product.
(a) (–9) × 5 × 6 × (–3)
The negative factors are (–9) and (–3). There are 2 negative factors (an even number).
The sign of the product is positive.
Value = $+810$
(b) 9 × (–5) × 6 × (–3)
The negative factors are (–5) and (–3). There are 2 negative factors (an even number).
The sign of the product is positive.
Value = $+810$
(c) (–9) × (–5) × (–6) × 3
The negative factors are (–9), (–5), and (–6). There are 3 negative factors (an odd number).
The sign of the product is negative.
Value = $-810$
(d) 9 × (–5) × (–6) × 3
The negative factors are (–5) and (–6). There are 2 negative factors (an even number).
The sign of the product is positive.
Value = $+810$
The values of options (a), (b), and (d) are all $+810$. The value of option (c) is $-810$, which is different.
The expression different from the others is (–9) × (–5) × (–6) × 3.
The correct answer is (c) (–9) × (–5) × (–6) × 3.
Question 29.
(a) (–100) ÷ 5
(b) (–81) ÷ 9
(c) (–75) ÷ 5
(d) (–32) ÷ 9
Answer:
Solution:
We are given four division expressions. We need to evaluate each expression to find their values and identify the one that is different from the others. In this case, since we are dealing with integers, 'different' might mean not an integer, or a different integer value.
Evaluate option (a): $(–100) \div 5$
When a negative integer is divided by a positive integer, the result is a negative integer.
$(-100) \div 5 = -(100 \div 5) = -20$
Evaluate option (b): $(–81) \div 9$
When a negative integer is divided by a positive integer, the result is a negative integer.
$(-81) \div 9 = -(81 \div 9) = -9$
Evaluate option (c): $(–75) \div 5$
When a negative integer is divided by a positive integer, the result is a negative integer.
$(-75) \div 5 = -(75 \div 5) = -15$
Evaluate option (d): $(–32) \div 9$
When a negative integer is divided by a positive integer, the result is a negative number. We check if the result is an integer.
$-32 \div 9 = -\frac{32}{9}$
Since 32 is not divisible by 9 without a remainder, the result is a fraction or a non-terminating decimal ($-\frac{32}{9} \approx -3.55$). This is not an integer.
Options (a), (b), and (c) result in integers ($-20, -9, -15$ respectively). Option (d) results in a number that is not an integer.
Therefore, $(–32) \div 9$ is different from the others.
The correct answer is (d) (–32) ÷ 9.
Question 30.
(a) (–1) × (–1)
(b) (–1) × (–1) × (–1)
(c) (–1) × (–1) × (–1) × (–1)
(d) (–1) × (–1) × (–1) × (–1) × (–1) × (–1)
Answer:
Solution:
We need to evaluate each expression and find the one that results in a different value from the others.
Recall that the product of an even number of negative signs is positive, and the product of an odd number of negative signs is negative.
Evaluate option (a): $(–1) \times (–1)$
There are two negative factors (an even number).
$(-1) \times (-1) = 1$
Evaluate option (b): $(–1) \times (–1) \times (–1)$
There are three negative factors (an odd number).
$(-1) \times (-1) \times (-1) = (1) \times (-1) = -1$
Evaluate option (c): $(–1) \times (–1) \times (–1) \times (–1)$
There are four negative factors (an even number).
$(-1) \times (-1) \times (-1) \times (-1) = (1) \times (1) = 1$
Evaluate option (d): $(–1) \times (–1) \times (–1) \times (–1) \times (–1) \times (–1)$
There are six negative factors (an even number).
$(-1) \times (-1) \times (-1) \times (-1) \times (-1) \times (-1) = (1) \times (1) \times (1) = 1$
Comparing the results:
(a) Value = $1$
(b) Value = $-1$
(c) Value = $1$
(d) Value = $1$
The values of options (a), (c), and (d) are all $1$. The value of option (b) is $-1$, which is different.
The expression different from the others is $(–1) \times (–1) \times (–1)$.
The correct answer is (b) (–1) × (–1) × (–1).
Question 31 to 71 (Fill in the Blanks)
In Questions 31 to 71, fill in the blanks to make the statements true.
Question 31. (–a) + b = b + Additive inverse of __________.
Answer:
The given statement is:
$(-a) + b = b + \text{Additive inverse of __________}$
We know that addition is commutative. This means that for any two numbers $x$ and $y$, the order of addition does not matter, i.e., $x + y = y + x$.
Applying the commutative property to the left side of the given statement, we can write:
$(-a) + b = b + (-a)$
Now, comparing the equation $b + (-a)$ with the right side of the given statement, which is $b + \text{Additive inverse of __________}$, we can infer that the expression $\text{Additive inverse of __________}$ must be equal to $(-a)$.
Let the required term in the blank be $x$.
According to the statement, the additive inverse of $x$ is equal to $-a$.
$\text{Additive inverse of } x = -a$
By the definition of additive inverse, the additive inverse of $x$ is $-x$.
So, we have:
$-x = -a$
Multiplying both sides of the equation by $-1$, we get:
$-1 \times (-x) = -1 \times (-a)$
$x = a$
Thus, the blank should be filled with $a$.
The complete statement is $(-a) + b = b + \text{Additive inverse of } a$. This is correct because the additive inverse of $a$ is $-a$, and $(-a) + b = b + (-a)$ by the commutative property of addition.
The final answer is $a$.
Question 32. ________ ÷ (–10) = 0
Answer:
The given equation is:
$\text{__________} \div (-10) = 0$
Let the missing number be $x$. The equation can be written as:
$\frac{x}{-10} = 0$
To find the value of $x$, we multiply both sides of the equation by $-10$.
$\frac{x}{-10} \times (-10) = 0 \times (-10)$
$x = 0$
Any number divided by zero is undefined, but zero divided by any non-zero number is zero. In this case, the divisor is $-10$, which is non-zero. Therefore, the only number that can be divided by $-10$ to give a result of $0$ is $0$ itself.
Thus, the blank should be filled with $0$.
The complete statement is $0 \div (-10) = 0$.
The final answer is $0$.
Question 33. (–157) × (–19) + 157 = ___________
Answer:
The given expression is:
$(-157) \times (-19) + 157$
We can solve this expression using the order of operations (PEMDAS/BODMAS), which dictates that multiplication should be performed before addition.
First, calculate the product of $(-157)$ and $(-19)$.
When multiplying two negative numbers, the result is a positive number.
$(\text{negative}) \times (\text{negative}) = (\text{positive})$
$(-157) \times (-19) = 157 \times 19$
Let's multiply 157 by 19:
$\begin{array}{cc}& & 1 & 5 & 7 \\ \times & & & 1 & 9 \\ \hline && 1 & 4 & 1 & 3 \\ & 1 & 5 & 7 & \times \\ \hline 2 & 9 & 8 & 3 \\ \hline \end{array}$
So, $(-157) \times (-19) = 2983$.
Now, substitute this value back into the original expression:
$2983 + 157$
Let's perform the addition:
$\begin{array}{cc} & 2 & 9 & 8 & 3 \\ + & & 1 & 5 & 7 \\ \hline & 3 & 1 & 4 & 0 \\ \hline \end{array}$
So, $2983 + 157 = 3140$.
Alternatively, we can use the distributive property.
The expression is $(-157) \times (-19) + 157$.
We can rewrite $157$ as $157 \times 1$.
So the expression becomes $(-157) \times (-19) + 157 \times 1$.
We can also write $-157$ as $157 \times (-1)$.
The expression is $157 \times (-1) \times (-19) + 157 \times 1$.
Using the associative property of multiplication, this is $157 \times ((-1) \times (-19)) + 157 \times 1$.
$(-1) \times (-19) = 19$.
So, the expression is $157 \times 19 + 157 \times 1$.
Now, using the distributive property $a \times b + a \times c = a \times (b + c)$, we factor out $157$:
$157 \times (19 + 1)$
Perform the addition inside the parenthesis:
$157 \times 20$
Now, multiply 157 by 20:
$157 \times 20 = 157 \times 2 \times 10 = 314 \times 10 = 3140$
Both methods yield the same result.
Thus, the blank should be filled with $3140$.
The complete statement is $(-157) \times (-19) + 157 = 3140$.
The final answer is $3140$.
Question 34. [(–8) + ______ ] + ________ = ________ + [(–3) + ________ ] = –3
Answer:
Solution:
The given equation is:
$[(-8) + \text{______} ] + \text{________} = \text{________} + [(-3) + \text{________} ] = –3$
This equation demonstrates the associative property of addition, which states that for any three numbers $a, b, c$, the grouping of the numbers does not affect the sum: $(a+b)+c = a+(b+c)$.
Let the three numbers being added be $n_1, n_2, n_3$. The equation implies that their sum is $-3$. So, $n_1 + n_2 + n_3 = -3$.
Comparing the left side of the equation, $[(-8) + \text{Blank 1}] + \text{Blank 2}$, with the form $(a+b)+c$, we identify that one of the numbers is $-8$. Let $a=-8$. Then the numbers involved are $-8$, Blank 1, and Blank 2. The structure suggests $b = \text{Blank 1}$ and $c = \text{Blank 2}$. The set of numbers on the left is $\{-8, \text{Blank 1}, \text{Blank 2}\}$.
Comparing the middle part of the equation, $\text{Blank 3} + [(-3) + \text{Blank 4}]$, with the form $a+(b+c)$, we identify that one of the numbers is $-3$. Let $b=-3$. Then the numbers involved are Blank 3, $-3$, and Blank 4. The structure suggests $a = \text{Blank 3}$ and $c = \text{Blank 4}$. The set of numbers on the right is $\{\text{Blank 3}, -3, \text{Blank 4}\}$.
Since the equation shows the associative property applied to the same set of numbers, the set $\{-8, \text{Blank 1}, \text{Blank 2}\}$ must be the same as the set $\{\text{Blank 3}, -3, \text{Blank 4}\}$. This common set contains the three numbers whose sum is $-3$.
We know that $-8$ and $-3$ are two of these numbers. Let the third number in the set be $k$. The sum is:
$(-8) + (-3) + k = -3$
$-11 + k = -3$
$k = -3 + 11$
$k = 8$
So, the three numbers being added are $-8$, $-3$, and $8$. The set of numbers is $\{-8, -3, 8\}$.
Now, we match these numbers to the blank positions based on the structure $(a+b)+c = a+(b+c)$ where the numbers are $a, b, c$ from the set $\{-8, -3, 8\}$.
From the left side structure $[(-8) + \text{Blank 1}] + \text{Blank 2}$, comparing with $(a+b)+c$:
We can set $a=-8$. Then the expression is $(-8 + b) + c$.
Comparing with $[(-8) + \text{Blank 1}] + \text{Blank 2}]$, we get:
Blank 1 = $b$
Blank 2 = $c$
So, the set $\{b, c\}$ must contain the remaining numbers from $\{-8, -3, 8\}$ after taking $a=-8$, which are $\{-3, 8\}$.
From the right side structure $\text{Blank 3} + [(-3) + \text{Blank 4}]$, comparing with $a+(b+c)$:
We can set $b=-3$. Then the expression is $a + (-3 + c)$.
Comparing with $\text{Blank 3} + [(-3) + \text{Blank 4}]$, we get:
Blank 3 = $a$
Blank 4 = $c$
So, the set $\{a, c\}$ must contain the remaining numbers from $\{-8, -3, 8\}$ after taking $b=-3$, which are $\{-8, 8\}$.
To fit the exact structure $(a+b)+c = a+(b+c)$:
Let $a=-8$, $b=-3$, and $c=8$. The associative property states $(a+b)+c = a+(b+c)$.
Substituting these values:
$((-8) + (-3)) + 8 = -8 + (-3 + 8)$
Comparing the left side with $[(-8) + \text{Blank 1}] + \text{Blank 2}]$:
$(-8 + (-3)) + 8 \implies$ Blank 1 = $-3$, Blank 2 = $8$.
Comparing the right side with $\text{Blank 3} + [(-3) + \text{Blank 4}]$:
$-8 + (-3 + 8) \implies$ Blank 3 = $-8$, Blank 4 = $8$.
Thus, the blanks are filled as follows:
Blank 1: $-3$
Blank 2: $8$
Blank 3: $-8$
Blank 4: $8$
Substituting these back into the original statement:
$[(-8) + (-3) ] + 8 = -8 + [(-3) + 8 ] = –3$
$[-11] + 8 = -8 + [5] = -3$
$-3 = -3 = -3$
The final answer is $\text{ Blank 1} = -3$, $\text{ Blank 2} = 8$, $\text{ Blank 3} = -8$, $\text{ Blank 4} = 8$.
Question 35. On the following number line, (–4) × 3 is represented by the point _________.

Answer:
Solution:
The given expression is $(–4) \times 3$.
We need to calculate the value of this expression.
$(–4) \times 3 = - (4 \times 3)$
$- (4 \times 3) = -12$
So, $(–4) \times 3 = -12$.
Now, we need to find the point on the given number line that represents the value $-12$.
Looking at the number line provided in the image:
- The point labeled O is at 0.
- Points to the right of O represent positive numbers: G (3), F (6), E (9), D (12), C (15).
- Points to the left of O represent negative numbers: H (-3), I (-6), J (-9), K (-12), L (-15).
The point representing $-12$ on this number line is labeled K.
Thus, $(–4) \times 3$ is represented by the point K.
The complete statement is: On the following number line, (–4) × 3 is represented by the point K.
The final answer is K.
Question 36. If x, y and z are integers then (x + ___ ) + z = _____ + (y + _____ )
Answer:
Solution:
The given statement is:
If x, y and z are integers then (x + ______ ) + ________ = ________ + (y + ______ )
This statement represents the associative property of addition for integers. The associative property states that for any three integers $a$, $b$, and $c$, the grouping of the numbers in addition does not change the sum. Mathematically, this is expressed as:
$(a + b) + c = a + (b + c)$
Comparing the left side of the given equation, $(x + \text{Blank 1}) + \text{Blank 2}$, with the form $(a + b) + c$, where the numbers involved are $x, y, z$, we can identify the parts.
If we consider the standard form $(x + y) + z$, then $a=x$, $b=y$, and $c=z$.
Matching $(x + \text{Blank 1}) + \text{Blank 2}$ with $(x + y) + z$, we see that:
Blank 1 corresponds to $y$.
Blank 2 corresponds to $z$.
Comparing the right side of the given equation, $\text{Blank 3} + (y + \text{Blank 4})$, with the form $a + (b + c)$, where the numbers involved are $x, y, z$, we can identify the parts.
If we consider the standard form $x + (y + z)$, then $a=x$, $b=y$, and $c=z$.
Matching $\text{Blank 3} + (y + \text{Blank 4})$ with $x + (y + z)$, we see that:
Blank 3 corresponds to $x$.
Blank 4 corresponds to $z$.
So, the blanks should be filled as follows:
First blank: $y$
Second blank: $z$ (This blank appears after the first grouping)
Third blank: $x$ (This blank appears before the second grouping)
Fourth blank: $z$ (This blank appears inside the second grouping)
The complete statement is:
If x, y and z are integers then (x + $y$ ) + $z$ = $x$ + (y + $z$ )
This is indeed the associative property of addition: $(x + y) + z = x + (y + z)$.
The final answer is $y$, $z$, $x$, $z$.
Question 37. (– 43) + _____ = – 43
Answer:
Solution:
The given equation is:
$(-43) + \text{______} = –43$
This equation demonstrates the property of the additive identity.
The additive identity is a number which, when added to any number, leaves the original number unchanged.
For any number $a$, the additive identity is 0, because $a + 0 = a$ and $0 + a = a$.
In the given equation, we have $(-43) + \text{Blank} = -43$.
Comparing this with the property $a + \text{Identity} = a$, where $a = -43$, we see that the value in the blank must be the additive identity.
Thus, the number that should fill the blank is 0.
$-43 + 0 = -43$
Alternatively, let the blank be $x$. The equation is:
$-43 + x = -43$
To solve for $x$, add $43$ (the additive inverse of $-43$) to both sides of the equation:
$-43 + x + 43 = -43 + 43$
$( -43 + 43 ) + x = 0$
$0 + x = 0$
$x = 0$
Thus, the blank should be filled with $0$.
The complete statement is $(– 43) + 0 = – 43$.
The final answer is $0$.
Question 38. (– 8) + (– 8) + (– 8) = _____ × (– 8)
Answer:
Solution:
The given equation is:
$(-8) + (-8) + (-8) = \text{______} \times (-8)$
The left side of the equation represents the repeated addition of the number $-8$.
Adding $-8$ to itself three times is equivalent to multiplying $-8$ by the number of times it is added.
In this case, $-8$ is added 3 times.
$(– 8) + (– 8) + (– 8) = 3 \times (– 8)$
The right side of the equation is $\text{______} \times (-8)$.
Comparing $3 \times (-8)$ with $\text{______} \times (-8)$, we can see that the blank should be filled with $3$.
Let's verify the equality:
Left side: $(-8) + (-8) + (-8) = -16 + (-8) = -24$.
Right side: $3 \times (-8) = -24$.
Since $-24 = -24$, the equality holds true when the blank is filled with 3.
Alternatively, let the blank be $x$. The equation is:
$-8 + (-8) + (-8) = x \times (-8)$
Calculate the left side:
$-24 = x \times (-8)$
To solve for $x$, divide both sides of the equation by $-8$ (since $-8 \neq 0$).
$\frac{-24}{-8} = \frac{x \times (-8)}{-8}$
$\frac{-24}{-8} = x$
When dividing two numbers with the same sign (both negative), the result is positive.
$x = \frac{24}{8}$
$x = 3$
Thus, the blank should be filled with $3$.
The complete statement is $(– 8) + (– 8) + (– 8) = 3 \times (– 8)$.
The final answer is $3$.
Question 39. 11 × (– 5) = – ( _____ × _____ ) = _____
Answer:
Solution:
The given equation is:
$11 \times (– 5) = – ( \text{_____} \times \text{_____} ) = \text{_____}$
First, let's calculate the product $11 \times (-5)$.
When a positive number is multiplied by a negative number, the result is a negative number.
Positive $\times$ Negative = Negative
$11 \times (-5) = -(11 \times 5)$
$-(11 \times 5) = -55$
So, $11 \times (-5) = -55$. This value will be the final result after the second equals sign.
Now consider the middle part of the equation: $– ( \text{_____} \times \text{_____} )$.
This structure suggests that the negative sign is taken out, and the multiplication inside the parenthesis involves the absolute values of the numbers being multiplied.
The absolute value of 11 is $|11| = 11$.
The absolute value of $-5$ is $|-5| = 5$.
So, the multiplication inside the parenthesis should be the product of their absolute values.
$- ( \text{_____} \times \text{____} ) = - ( 11 \times 5 )$
Let's verify this:
$- (11 \times 5) = -(55) = -55$
This matches the calculated product $11 \times (-5)$.
Thus, the blanks should be filled as follows:
The first blank inside the parenthesis is $11$.
The second blank inside the parenthesis is $5$.
The blank after the second equals sign is $-55$.
The complete statement is $11 \times (– 5) = – ( 11 \times 5 ) = – 55$.
The final answer is $11$, $5$, $-55$.
Question 40. (– 9) × 20 = _____
Answer:
Solution:
The given equation is:
$(-9) \times 20 = \text{______}$
We need to calculate the product of $-9$ and $20$.
When multiplying a negative number by a positive number, the result is a negative number.
Negative $\times$ Positive = Negative
$(-9) \times 20 = -(9 \times 20)$
Now, calculate the product of the absolute values:
$9 \times 20 = 180$
Substitute this back into the expression:
$-(9 \times 20) = -180$
So, $(-9) \times 20 = -180$.
Thus, the blank should be filled with $-180$.
The complete statement is $(– 9) \times 20 = – 180$.
The final answer is $-180$.
Question 41. (– 23) × (42) = (– 42) × _____
Answer:
Solution:
The given equation is:
$(-23) \times (42) = (-42) \times \text{______}$
We need to find the number that fills the blank to make the statement true.
Let the number in the blank be $x$. The equation is:
$-23 \times 42 = -42 \times x$
First, let's calculate the product on the left side:
$-23 \times 42$
The product of a negative integer and a positive integer is a negative integer.
$-(23 \times 42)$
Calculating the product $23 \times 42$:
$\begin{array}{cc}& & 2 & 3 \\ \times & & 4 & 2 \\ \hline & & 4 & 6 \\ 9 & 2 & \times \\ \hline 9 & 6 & 6 \\ \hline \end{array}$
So, $23 \times 42 = 966$.
Therefore, $-23 \times 42 = -966$.
Now, the equation becomes:
$-966 = -42 \times x$
To find the value of $x$, we need to isolate $x$. We can do this by dividing both sides of the equation by $-42$ (since $-42 \neq 0$).
$\frac{-966}{-42} = \frac{-42 \times x}{-42}$
$\frac{-966}{-42} = x$
The division of two negative integers results in a positive integer.
$x = \frac{966}{42}$
Let's perform the division $966 \div 42$.
$\frac{966}{42} = \frac{\cancel{966}^{483}}{\cancel{42}_{21}}$ (Dividing numerator and denominator by 2)
Now divide 483 by 21. Both are divisible by 3 (sum of digits of 483 is 15, sum of digits of 21 is 3).
$\frac{483}{21} = \frac{\cancel{483}^{161}}{\cancel{21}_{7}}$ (Dividing numerator and denominator by 3)
Now divide 161 by 7.
$161 \div 7 = 23$
So, $x = 23$.
Thus, the blank should be filled with $23$.
The complete statement is $(– 23) \times (42) = (– 42) \times 23$.
This is true because $(-23) \times 42 = -966$ and $(-42) \times 23 = -966$.
The final answer is $23$.
Question 42. While multiplying a positive integer and a negative integer, we multiply them as ________ numbers and put a ________ sign before the product.
Answer:
Solution:
The statement describes the process of multiplying a positive integer and a negative integer.
Consider the multiplication of a positive integer $a$ (where $a > 0$) and a negative integer $b$ (where $b < 0$).
The product $a \times b$ is calculated in two steps:
- Multiply the absolute values of the two integers. The absolute value of a positive integer is the integer itself, and the absolute value of a negative integer is its positive counterpart. So, we calculate $|a| \times |b|$. Since $a$ is positive, $|a| = a$. Since $b$ is negative, $|b| = -b$ (which is a positive number). The product of their absolute values is $a \times (-b)$. This step is multiplying two positive numbers.
- Place a negative sign before the result obtained in step 1.
So, $a \times b = -(a \times |b|)$. Since $a > 0$ and $b < 0$, we have $|a| = a$ and $|b| = -b$. Thus, $a \times b = -(a \times (-b))$. Wait, this is not quite right based on the standard rule. The standard rule is $a \times (-b) = -(a \times b)$.
Let's rephrase based on the blanks provided.
"While multiplying a positive integer and a negative integer, we multiply them as ________ numbers..." This refers to multiplying their magnitudes, ignoring the signs initially. The magnitudes are the absolute values, which are always non-negative (and positive if the original numbers are non-zero). So, we multiply the absolute values, which are positive numbers.
"...and put a ________ sign before the product." The product of a positive and a negative integer is always negative.
Let's illustrate with an example: $5 \times (-3)$.
- Multiply them as positive numbers: Multiply the absolute values $|5|$ and $|-3|$, which are 5 and 3. $5 \times 3 = 15$.
- Put a negative sign before the product: $-15$.
So, $5 \times (-3) = -15$.
Based on this rule:
- The first blank: "we multiply them as ________ numbers". We multiply their absolute values, which are positive numbers. So the blank should be filled with positive.
- The second blank: "and put a ________ sign before the product". The sign is negative. So the blank should be filled with negative.
The complete statement is: While multiplying a positive integer and a negative integer, we multiply them as positive numbers and put a negative sign before the product.
The final answer is positive, negative.
Question 43. If we multiply ________ number of negative integers, then the resulting integer is positive.
Answer:
Solution:
The statement is about the sign of the product when multiplying negative integers.
Let's consider the sign of the product based on the number of negative integers being multiplied:
- When we multiply one negative integer, the sign is negative. For example, $(-5) = -5$.
- When we multiply two negative integers, the sign is positive. For example, $(-2) \times (-3) = 6$.
- When we multiply three negative integers, the sign is negative. For example, $(-2) \times (-3) \times (-4) = 6 \times (-4) = -24$.
- When we multiply four negative integers, the sign is positive. For example, $(-2) \times (-3) \times (-4) \times (-5) = -24 \times (-5) = 120$.
We observe a pattern:
- An odd number of negative integers multiplied results in a negative product.
- An even number of negative integers multiplied results in a positive product.
The statement says that the resulting integer is positive.
According to our observation, this happens when the number of negative integers being multiplied is even.
Thus, the blank should be filled with even.
The complete statement is: If we multiply even number of negative integers, then the resulting integer is positive.
The final answer is even.
Question 44. If we multiply six negative integers and six positive integers, then the resulting integer is _______.
Answer:
Solution:
The statement asks for the sign of the resulting integer when multiplying six negative integers and six positive integers.
First, consider the product of the six negative integers.
When multiplying negative integers:
- An odd number of negative integers results in a negative product.
- An even number of negative integers results in a positive product.
Since we are multiplying six negative integers, and six is an even number, the product of these six negative integers will be positive.
Next, consider the product of the six positive integers.
When multiplying positive integers, the product is always positive, regardless of the number of integers.
Finally, we are multiplying the product of the six negative integers (which is positive) by the product of the six positive integers (which is positive).
The product of a positive number and a positive number is always positive.
Positive $\times$ Positive = Positive
Therefore, the resulting integer will be positive.
Thus, the blank should be filled with positive.
The complete statement is: If we multiply six negative integers and six positive integers, then the resulting integer is positive.
The final answer is positive.
Question 45. If we multiply five positive integers and one negative integer, then the resulting integer is _______.
Answer:
Solution:
The statement asks for the sign of the resulting integer when multiplying five positive integers and one negative integer.
First, consider the product of the five positive integers.
The product of any number of positive integers is always positive.
Next, consider the one negative integer. This integer is simply negative.
Finally, we are multiplying the product of the five positive integers (which is positive) by the one negative integer (which is negative).
The product of a positive number and a negative number is always negative.
Positive $\times$ Negative = Negative
Therefore, the resulting integer will be negative.
Thus, the blank should be filled with negative.
The complete statement is: If we multiply five positive integers and one negative integer, then the resulting integer is negative.
The final answer is negative.
Question 46. __________ is the multiplicative identity for integers.
Answer:
Solution:
The given statement is:
__________ is the multiplicative identity for integers.
We need to identify the number that, when multiplied by any integer, leaves the integer unchanged.
This property is called the multiplicative identity property.
For any integer $a$, the multiplicative identity $e$ must satisfy the equation:
$a \times e = a$
and
$e \times a = a$
Let's test some integers:
- If $a = 5$, then $5 \times e = 5$. Dividing both sides by 5 (since $5 \neq 0$), we get $e = \frac{5}{5} = 1$.
- If $a = -7$, then $-7 \times e = -7$. Dividing both sides by -7 (since $-7 \neq 0$), we get $e = \frac{-7}{-7} = 1$.
- If $a = 0$, then $0 \times e = 0$. This equation is true for any value of $e$. However, the identity must work for all integers.
The only number that satisfies $a \times e = a$ for all non-zero integers $a$ is $e=1$. We also check if $1$ works for $a=0$: $0 \times 1 = 0$, which is true. Thus, the multiplicative identity for integers is $1$.
The number that fits this description is 1.
Thus, the blank should be filled with 1.
The complete statement is 1 is the multiplicative identity for integers.
The final answer is 1.
Question 47. We get additive inverse of an integer a when we multiply it by ________.
Answer:
Solution:
The statement asks for the number that, when multiplied by an integer $a$, results in the additive inverse of $a$.
The additive inverse of an integer $a$ is the integer $-a$. This is because $a + (-a) = 0$.
We are looking for a number, let's call it $x$, such that when we multiply $a$ by $x$, we get the additive inverse of $a$.
This can be written as an equation:
$a \times x = -a$
We need to find the value of $x$ that satisfies this equation for any integer $a$.
Consider the case where $a$ is a non-zero integer (if $a=0$, the additive inverse is 0, and $0 \times x = 0$ is true for any $x$. But the property must hold for all integers $a$).
If $a \neq 0$, we can divide both sides of the equation by $a$ to solve for $x$:
$\frac{a \times x}{a} = \frac{-a}{a}$
$x = -1$
Let's verify this with an example. Let $a = 5$. The additive inverse of 5 is $-5$. Multiplying 5 by $-1$ gives $5 \times (-1) = -5$, which is the additive inverse.
Let $a = -10$. The additive inverse of $-10$ is $-(-10) = 10$. Multiplying $-10$ by $-1$ gives $(-10) \times (-1) = 10$, which is the additive inverse.
Consider the case where $a=0$. The additive inverse of 0 is $-0 = 0$. Multiplying 0 by $-1$ gives $0 \times (-1) = 0$, which is the additive inverse.
So, multiplying by $-1$ gives the additive inverse for all integers.
Thus, the blank should be filled with $-1$.
The complete statement is: We get additive inverse of an integer a when we multiply it by $-1$.
The final answer is $-1$.
Question 48. (– 25) × (– 2) = __________.
Answer:
Solution:
The given equation is:
$(-25) \times (-2) = \text{__________}$
We need to calculate the product of $-25$ and $-2$.
When multiplying two negative integers, the result is a positive integer.
Negative $\times$ Negative = Positive
The product is obtained by multiplying the absolute values of the two integers and placing a positive sign (or no sign) before the result.
$(-25) \times (-2) = |{-25}| \times |{-2}|$
$|{-25}| = 25$
$|{-2}| = 2$
Now, multiply the absolute values:
$25 \times 2 = 50$
So, the product of $(-25)$ and $(-2)$ is $50$.
Thus, the blank should be filled with $50$.
The complete statement is $(– 25) \times (– 2) = 50$.
The final answer is $50$.
Question 49. (– 5) × (– 6) × (– 7) = ________.
Answer:
The given expression is:
$(-5) \times (-6) \times (-7) = \text{__________}$
We need to calculate the product of these three negative integers.
We can multiply the integers step by step.
First, multiply the first two integers: $(-5) \times (-6)$.
The product of two negative integers is a positive integer.
$(-5) \times (-6) = |{-5}| \times |{-6}| = 5 \times 6 = 30$
Now, multiply the result, 30, by the third integer, $(-7)$.
$30 \times (-7)$
The product of a positive integer and a negative integer is a negative integer.
$30 \times (-7) = -(30 \times 7)$
$-(30 \times 7) = -210$
So, $(-5) \times (-6) \times (-7) = -210$.
Alternatively, we can determine the sign based on the number of negative integers being multiplied.
We are multiplying three negative integers: $(-5)$, $(-6)$, and $(-7)$.
The number of negative integers is 3, which is an odd number.
When an odd number of negative integers are multiplied, the result is negative.
The magnitude of the product is the product of the absolute values:
$|{-5}| \times |{-6}| \times |{-7}| = 5 \times 6 \times 7$
$5 \times 6 = 30$
$30 \times 7 = 210$
Since the resulting integer is negative, the product is $-210$.
Thus, the blank should be filled with $-210$.
The complete statement is $(– 5) \times (– 6) \times (– 7) = – 210$.
The final answer is $-210$.
Question 50. 3 × (– 1 ) × (– 15) = _______.
Answer:
Solution:
The given expression is:
$3 \times (– 1 ) \times (– 15) = \text{__________}$
We need to calculate the product of these three integers.
We can multiply the integers step by step.
First, multiply the first two integers: $3 \times (-1)$.
The product of a positive integer and a negative integer is a negative integer.
$3 \times (-1) = -(3 \times 1) = -3$
Now, multiply the result, $-3$, by the third integer, $(-15)$.
$(-3) \times (-15)$
The product of two negative integers is a positive integer.
$(-3) \times (-15) = |{-3}| \times |{-15}| = 3 \times 15 = 45$
So, $3 \times (-1) \times (-15) = 45$.
Alternatively, we can determine the sign first by counting the number of negative integers being multiplied.
We are multiplying $3$, $-1$, and $-15$. There are two negative integers ($-1$ and $-15$).
The number of negative integers is 2, which is an even number.
When an even number of negative integers are multiplied, the result is positive.
The magnitude of the product is the product of the absolute values:
$|3| \times |{-1}| \times |{-15}| = 3 \times 1 \times 15$
$3 \times 1 = 3$
$3 \times 15 = 45$
Since the resulting integer is positive, the product is $45$.
Thus, the blank should be filled with $45$.
The complete statement is $3 \times (– 1 ) \times (– 15) = 45$.
The final answer is $45$.
Question 51. [12 × (– 7)] × 5 = ________× [(– 7) × ]
Answer:
Solution:
The given equation is:
$[12 \times (– 7)] \times 5 = \text{__________}\times [(– 7) \times \text{__________}]$
This equation demonstrates the associative property of multiplication for integers. This property states that for any three integers $a$, $b$, and $c$, the grouping of the numbers in multiplication does not change the product. Mathematically, this is expressed as:
$(a \times b) \times c = a \times (b \times c)$
Comparing the left side of the given equation, $[12 \times (– 7)] \times 5$, with the form $(a \times b) \times c$, we can identify the three integers being multiplied as $12$, $-7$, and $5$. The grouping is $(12 \times (-7)) \times 5$. This matches the form $(a \times b) \times c$ where $a=12$, $b=-7$, and $c=5$.
Now, consider the right side of the given equation: $\text{Blank 1} \times [(- 7) \times \text{Blank 2}]$. This matches the form $a \times (b \times c)$.
From the left side, we know the three integers involved are $12, -7, 5$. The associative property means the right side uses the same three integers, just grouped differently.
Comparing $\text{Blank 1} \times [(- 7) \times \text{Blank 2}]$ with $a \times (b \times c)$, and knowing the numbers are $12, -7, 5$, we can match the parts:
- The number $-7$ is inside the parenthesis on the right side, just like $b$ and $c$ are inside the parenthesis in $a \times (b \times c)$. Specifically, it's one of the factors inside $[(-7) \times \text{Blank 2}]$. Let's assume the structure exactly follows $a \times (b \times c)$.
- The structure is $\text{Blank 1} \times [(-7) \times \text{Blank 2}]$. This fits the form $a \times (b \times c)$. The term outside the parenthesis is $\text{Blank 1}$, which corresponds to $a$. The terms inside the parenthesis are $-7$ and $\text{Blank 2}$, which correspond to $b$ and $c$ (or $c$ and $b$, as multiplication is commutative).
From the left side, $a=12$, $b=-7$, $c=5$. Applying the associative property, the right side should be $a \times (b \times c) = 12 \times ((-7) \times 5)$.
Comparing this with $\text{Blank 1} \times [(- 7) \times \text{Blank 2}]$:
$\text{Blank 1}$ corresponds to $12$.
The terms inside $[(-7) \times \text{Blank 2}]$ are $-7$ and $\text{Blank 2}$. In $12 \times ((-7) \times 5)$, the terms inside the parenthesis are $-7$ and $5$.
So, $\text{Blank 2}$ corresponds to $5$.
Thus, the blanks should be filled with:
First blank (before the parenthesis): $12$
Second blank (inside the parenthesis): $5$
The complete statement is $[12 \times (– 7)] \times 5 = 12 \times [(– 7) \times 5]$.
The final answer is $12$, $5$.
Question 52. 23 × (– 99) = _______ × (– 100 + _______) = 23 × _______ + 23 × _____.
Answer:
Solution:
The given equation is:
$23 \times (– 99) = \text{______} \times (– 100 + \text{_______}) = 23 \times \text{_______} + 23 \times \text{_____}.$
This equation involves the distributive property of multiplication over addition, which states that for any three integers $a$, $b$, and $c$, $a \times (b + c) = a \times b + a \times c$. It also implies that $a \times b + a \times c = a \times (b + c)$.
Let's analyze the equation part by part.
The first part is $23 \times (– 99)$.
The second part is $\text{Blank 1} \times (– 100 + \text{Blank 2})$.
The third part is $23 \times \text{Blank 3} + 23 \times \text{Blank 4}$.
Comparing the first part $23 \times (-99)$ with the structure $a \times (\text{sum})$, we can see that $a=23$. The sum inside the parenthesis should be equal to $-99$.
The second part is $\text{Blank 1} \times (-100 + \text{Blank 2})$. Comparing this with $a \times (b + c)$, we can identify $a = \text{Blank 1}$. Given that the first part is $23 \times (-99)$, and $a$ is the number being distributed, $\text{Blank 1}$ must be $23$.
So the equation becomes:
$23 \times (– 99) = 23 \times (– 100 + \text{Blank 2}) = 23 \times \text{Blank 3} + 23 \times \text{Blank 4}.$
Now, consider the part $23 \times (– 100 + \text{Blank 2})$. This must be equal to $23 \times (– 99)$.
By comparing $– 100 + \text{Blank 2}$ with $– 99$, we can find the value of Blank 2:
$-100 + \text{Blank 2} = -99$
Adding 100 to both sides of the equation:
$\text{Blank 2} = -99 + 100$
$\text{Blank 2} = 1$
So the second part is $23 \times (-100 + 1)$.
Now consider the third part: $23 \times \text{Blank 3} + 23 \times \text{Blank 4}$. This is the result of applying the distributive property to $23 \times (-100 + 1)$.
Using the distributive property $a \times (b + c) = a \times b + a \times c$, with $a=23$, $b=-100$, and $c=1$, we get:
$23 \times (-100 + 1) = 23 \times (-100) + 23 \times 1$
Comparing this with $23 \times \text{Blank 3} + 23 \times \text{Blank 4}$, we can see that:
Blank 3 must be $-100$.
Blank 4 must be $1$.
So, the blanks are filled as follows:
- First blank: $23$
- Second blank: $1$
- Third blank: $-100$
- Fourth blank: $1$
The complete statement is:
$23 \times (– 99) = 23 \times (– 100 + 1) = 23 \times (– 100) + 23 \times 1.$
Let's verify the equality by calculating the value of each part:
Part 1: $23 \times (-99) = -(23 \times 99) = -2277$.
Part 2: $23 \times (-100 + 1) = 23 \times (-99) = -2277$.
Part 3: $23 \times (-100) + 23 \times 1 = -2300 + 23 = -2277$.
All parts are equal to $-2277$, so the blanks are filled correctly.
The final answer is $23$, $1$, $-100$, $1$.
Question 53. __________ × ( – 1) = – 35
Answer:
Solution:
The given equation is:
$\text{__________} \times ( – 1) = – 35$
Let the missing number be $x$. The equation is:
$x \times (-1) = -35$
We know that multiplying any number by $-1$ gives its additive inverse (opposite sign).
So, the number $x$, when multiplied by $-1$, results in $-35$. This means that $-35$ is the additive inverse of $x$.
If $-35$ is the additive inverse of $x$, then $x$ must be the number whose additive inverse is $-35$.
The additive inverse of $-35$ is $-(-35) = 35$.
Therefore, $x = 35$.
Alternatively, to solve the equation $x \times (-1) = -35$ for $x$, we can divide both sides by $-1$ (since $-1 \neq 0$).
$\frac{x \times (-1)}{-1} = \frac{-35}{-1}$
$x = \frac{-35}{-1}$
The division of two negative numbers results in a positive number.
$x = \frac{35}{1}$
$x = 35$
Thus, the blank should be filled with $35$.
The complete statement is $35 \times ( – 1) = – 35$.
The final answer is $35$.
Question 54. ________× ( – 1) = 47
Answer:
Solution:
The given equation is:
$\text{__________} \times ( – 1) = 47$
Let the missing number be $x$. The equation is:
$x \times (-1) = 47$
We know that multiplying any number by $-1$ gives its additive inverse (opposite sign).
So, the number $x$, when multiplied by $-1$, results in $47$. This means that $47$ is the additive inverse of $x$.
If $47$ is the additive inverse of $x$, then $x$ must be the number whose additive inverse is $47$.
The additive inverse of $47$ is $-47$.
Therefore, $x = -47$.
Alternatively, to solve the equation $x \times (-1) = 47$ for $x$, we can divide both sides by $-1$ (since $-1 \neq 0$).
$\frac{x \times (-1)}{-1} = \frac{47}{-1}$
$x = \frac{47}{-1}$
The division of a positive number by a negative number results in a negative number.
$x = -( \frac{47}{1} )$
$x = -47$
Thus, the blank should be filled with $-47$.
The complete statement is $-47 \times ( – 1) = 47$.
The final answer is $-47$.
Question 55. 88 × _______ = – 88
Answer:
Solution:
The given equation is:
$88 \times \text{______} = – 88$
We need to find the number that, when multiplied by $88$, results in $-88$.
Let the missing number be $x$. The equation is:
$88 \times x = -88$
We observe that the result $-88$ is the additive inverse of the number $88$.
We know that multiplying any integer by $-1$ gives its additive inverse.
So, if we multiply $88$ by $-1$, we get $88 \times (-1) = -88$.
Comparing this with the given equation $88 \times x = -88$, we can see that $x$ must be $-1$.
Alternatively, to solve the equation $88 \times x = -88$ for $x$, we can divide both sides by $88$ (since $88 \neq 0$).
$\frac{88 \times x}{88} = \frac{-88}{88}$
$x = \frac{-88}{88}$
The division of a negative number by a positive number results in a negative number.
$x = -( \frac{88}{88} )$
$x = -1$
Thus, the blank should be filled with $-1$.
The complete statement is $88 \times ( – 1) = – 88$.
The final answer is $-1$.
Question 56. _____× (–93) = 93
Answer:
Solution:
The given equation is:
$\text{__________} \times ( – 93) = 93$
We need to find the number that, when multiplied by $-93$, results in $93$.
Let the missing number be $x$. The equation is:
$x \times (-93) = 93$
We observe that the result $93$ is the additive inverse of the number $-93$.
We know that multiplying any integer by $-1$ gives its additive inverse.
So, if we multiply $-93$ by $-1$, we get $(-93) \times (-1) = 93$.
Comparing this with the given equation $x \times (-93) = 93$, we can see that $x$ must be $-1$.
Alternatively, to solve the equation $x \times (-93) = 93$ for $x$, we can divide both sides by $-93$ (since $-93 \neq 0$).
$\frac{x \times (-93)}{-93} = \frac{93}{-93}$
$x = \frac{93}{-93}$
The division of a positive number by a negative number results in a negative number.
$x = -( \frac{93}{93} )$
$x = -1$
Thus, the blank should be filled with $-1$.
The complete statement is $-1 \times (– 93) = 93$.
The final answer is $-1$.
Question 57. (– 40) × _______= 80
Answer:
Solution:
The given equation is:
$(-40) \times \text{______} = 80$
We need to find the number that, when multiplied by $-40$, results in $80$.
Let the missing number be $x$. The equation is:
$(-40) \times x = 80$
To find the value of $x$, we need to isolate $x$. We can do this by dividing both sides of the equation by $-40$ (since $-40 \neq 0$).
$\frac{(-40) \times x}{-40} = \frac{80}{-40}$
$x = \frac{80}{-40}$
The division of a positive number by a negative number results in a negative number.
$x = -( \frac{80}{40} )$
$x = -2$
Let's verify the solution:
$(-40) \times (-2) = 80$
This is true because the product of two negative numbers is positive ($40 \times 2 = 80$).
Thus, the blank should be filled with $-2$.
The complete statement is $(– 40) \times (– 2) = 80$.
The final answer is $-2$.
Question 58. ___________× (–23) = – 920
Answer:
Solution:
The given equation is:
$\text{__________} \times (–23) = – 920$
We need to find the number that, when multiplied by $-23$, results in $-920$.
Let the missing number be $x$. The equation is:
$x \times (-23) = -920$
To find the value of $x$, we need to isolate $x$. We can do this by dividing both sides of the equation by $-23$ (since $-23 \neq 0$).
$\frac{x \times (-23)}{-23} = \frac{-920}{-23}$
$x = \frac{-920}{-23}$
The division of two negative numbers results in a positive number.
$x = \frac{920}{23}$
Now, let's perform the division:
$920 \div 23$
$920 = 92 \times 10 = (23 \times 4) \times 10 = 23 \times 40$
$\frac{920}{23} = \frac{23 \times 40}{23} = 40$
So, $x = 40$.
Let's verify the solution:
$40 \times (-23) = -(40 \times 23) = -920$
This is true.
Thus, the blank should be filled with $40$.
The complete statement is $40 \times (–23) = – 920$.
The final answer is $40$.
Question 59. When we divide a negative integer by a positive integer, we divide them as whole numbers and put a _______ sign before quotient.
Answer:
Solution:
The statement describes the rule for dividing a negative integer by a positive integer.
Let's consider dividing a negative integer $a$ by a positive integer $b$, where $a < 0$ and $b > 0$. The quotient is $\frac{a}{b}$.
The statement says we divide them as whole numbers. This means we divide the absolute value of the negative integer by the absolute value of the positive integer.
Absolute value of $a$ is $|a|$ (which is a positive whole number since $a$ is a non-zero integer).
Absolute value of $b$ is $|b|$ (which is a positive whole number since $b$ is a non-zero integer).
So, the division as whole numbers is $|a| \div |b| = \frac{|a|}{|b|}$. This gives the magnitude of the quotient.
The second part of the statement says "and put a _______ sign before quotient".
We need to determine the sign of the quotient $\frac{a}{b}$ where $a < 0$ and $b > 0$.
The rule for dividing integers with different signs is that the quotient is always negative.
For example:
- $(-10) \div 2 = -5$
- $(-18) \div 6 = -3$
In both examples, the quotient is negative.
Therefore, the sign that should be put before the quotient is negative.
Thus, the blank should be filled with negative.
The complete statement is: When we divide a negative integer by a positive integer, we divide them as whole numbers and put a negative sign before quotient.
The final answer is negative.
Question 60. When –16 is divided by _________ the quotient is 4.
Answer:
Solution:
The given statement can be written as a division problem:
$-16 \div \text{__________} = 4$
Let the missing number be $x$. The equation is:
$\frac{-16}{x} = 4$
To solve for $x$, we can multiply both sides of the equation by $x$ (assuming $x \neq 0$):
$\frac{-16}{x} \times x = 4 \times x$
$-16 = 4x$
Now, divide both sides of the equation by 4 (since $4 \neq 0$):
$\frac{-16}{4} = \frac{4x}{4}$
$x = \frac{-16}{4}$
The division of a negative integer by a positive integer results in a negative integer.
$x = -( \frac{16}{4} )$
$x = -4$
Let's verify the solution by substituting $x = -4$ back into the original statement:
$-16 \div (-4)$
When a negative integer is divided by a negative integer, the quotient is positive. $|-16| = 16$ and $|-4| = 4$. $16 \div 4 = 4$.
$-16 \div (-4) = 4$
This matches the given quotient.
Thus, the blank should be filled with $-4$.
The complete statement is When –16 is divided by –4 the quotient is 4.
The final answer is $-4$.
Question 61. Division is the inverse operation of ____________.
Answer:
Solution:
The given statement is:
Division is the inverse operation of __________.
In mathematics, inverse operations are operations that undo each other.
- Addition is the inverse operation of subtraction ($a+b=c \implies c-b=a$).
- Subtraction is the inverse operation of addition ($a-b=c \implies c+b=a$).
- Multiplication is the inverse operation of division ($a \times b = c \implies \frac{c}{b} = a$, for $b \neq 0$).
- Division is the inverse operation of multiplication ($\frac{a}{b} = c \implies a = c \times b$).
For example, consider the multiplication $3 \times 4 = 12$. The corresponding division operations are $12 \div 4 = 3$ and $12 \div 3 = 4$. Division "undoes" the multiplication.
Similarly, consider the division $15 \div 5 = 3$. The corresponding multiplication operation is $3 \times 5 = 15$. Multiplication "undoes" the division.
Thus, division is the inverse operation of multiplication.
The blank should be filled with multiplication.
The complete statement is: Division is the inverse operation of multiplication.
The final answer is multiplication.
Question 62. 65 ÷ ( – 13) = ___________.
Answer:
Solution:
The given expression is:
$65 \div ( – 13) = \text{__________}$
We need to calculate the quotient when $65$ is divided by $-13$.
We are dividing a positive integer ($65$) by a negative integer ($-13$).
When a positive integer is divided by a negative integer, the quotient is a negative integer.
Positive $\div$ Negative = Negative
The magnitude of the quotient is obtained by dividing the absolute value of the dividend by the absolute value of the divisor.
$65 \div (– 13) = -( |65| \div |{-13}| )$
$|65| = 65$
$|{-13}| = 13$
Now, perform the division of the absolute values:
$65 \div 13 = 5$
Since the quotient is negative, we put a negative sign before the result:
$-(65 \div 13) = -5$
So, $65 \div ( – 13) = -5$.
Thus, the blank should be filled with $-5$.
The complete statement is $65 \div ( – 13) = – 5$.
The final answer is $-5$.
Question 63. (– 100) ÷ ( – 10) = _______.
Answer:
Solution:
The given expression is:
$(-100) \div ( – 10) = \text{__________}$
We need to calculate the quotient when $-100$ is divided by $-10$.
We are dividing a negative integer ($-100$) by a negative integer ($-10$).
When a negative integer is divided by a negative integer, the quotient is a positive integer.
Negative $\div$ Negative = Positive
The magnitude of the quotient is obtained by dividing the absolute value of the dividend by the absolute value of the divisor.
$(-100) \div (– 10) = |{-100}| \div |{-10}|$
$|{-100}| = 100$
$|{-10}| = 10$
Now, perform the division of the absolute values:
$100 \div 10 = 10$
Since the quotient is positive, the result is $10$.
So, $(-100) \div ( – 10) = 10$.
Thus, the blank should be filled with $10$.
The complete statement is $(– 100) \div ( – 10) = 10$.
The final answer is $10$.
Question 64. (– 225) ÷ 5 = ___________.
Answer:
Solution:
The given expression is:
$(-225) \div 5 = \text{__________}$
We need to calculate the quotient when $-225$ is divided by $5$.
We are dividing a negative integer ($-225$) by a positive integer ($5$).
When a negative integer is divided by a positive integer, the quotient is a negative integer.
Negative $\div$ Positive = Negative
The magnitude of the quotient is obtained by dividing the absolute value of the dividend by the absolute value of the divisor.
$(-225) \div 5 = -( |{-225}| \div |5| )$
$|{-225}| = 225$
$|5| = 5$
Now, perform the division of the absolute values:
$225 \div 5$
We can perform long division:
$\begin{array}{r} 45 \phantom{)} \\ 5{\overline{\smash{\big)}\,225\phantom{)}}} \\ \underline{-~\phantom{(}20\phantom{2)})} \\ 025\phantom{)} \\ \underline{-~\phantom{()}25\phantom{)}} \\ 0\phantom{)} \end{array}$So, $225 \div 5 = 45$.
Since the quotient is negative, we put a negative sign before the result:
$-(225 \div 5) = -45$
So, $(-225) \div 5 = -45$.
Thus, the blank should be filled with $-45$.
The complete statement is $(– 225) \div 5 = – 45$.
The final answer is $-45$.
Question 65. _____÷ (– 1 ) = – 83
Answer:
Solution:
The given equation is:
$\text{__________} \div ( – 1 ) = – 83$
Let the missing number be $x$. The equation is:
$\frac{x}{-1} = -83$
We know that dividing any number by $-1$ changes its sign.
So, the number $x$, when divided by $-1$, results in $-83$. This means that $-83$ is the result of changing the sign of $x$.
The number whose sign changed becomes $-83$ is the additive inverse of $-83$.
The additive inverse of $-83$ is $-(-83) = 83$.
Therefore, $x = 83$.
Alternatively, to solve the equation $\frac{x}{-1} = -83$ for $x$, we can multiply both sides by $-1$:
$\frac{x}{-1} \times (-1) = -83 \times (-1)$
$x = -83 \times (-1)$
The product of two negative numbers is a positive number.
$x = 83$
Let's verify the solution by substituting $x = 83$ back into the original statement:
$83 \div (-1)$
The division of a positive integer by a negative integer is a negative integer. The magnitude is $83 \div 1 = 83$.
$83 \div (-1) = -83$
This matches the given quotient.
Thus, the blank should be filled with $83$.
The complete statement is $83 \div (– 1 ) = – 83$.
The final answer is $83$.
Question 66. _____ ÷ (– 1) = 75
Answer:
Solution:
The given equation is:
$\text{__________} \div ( – 1) = 75$
Let the missing number be $x$. The equation is:
$\frac{x}{-1} = 75$
We know that dividing any number by $-1$ changes its sign (gives its additive inverse). For example, $5 \div (-1) = -5$ and $(-10) \div (-1) = 10$.
So, the number $x$, when divided by $-1$, results in $75$. This means that $75$ is the result of changing the sign of $x$.
The number whose sign changed becomes $75$ is the additive inverse of $75$.
The additive inverse of $75$ is $-75$.
Therefore, $x = -75$.
Alternatively, to solve the equation $\frac{x}{-1} = 75$ for $x$, we can multiply both sides by $-1$:
$\frac{x}{-1} \times (-1) = 75 \times (-1)$
$x = 75 \times (-1)$
The product of a positive number and a negative number is a negative number.
$x = -(75 \times 1)$
$x = -75$
Let's verify the solution by substituting $x = -75$ back into the original statement:
$-75 \div (-1)$
The division of a negative integer by a negative integer is a positive integer. The magnitude is $|-75| \div |-1| = 75 \div 1 = 75$.
$-75 \div (-1) = 75$
This matches the given quotient.
Thus, the blank should be filled with $-75$.
The complete statement is $-75 \div (– 1) = 75$.
The final answer is $-75$.
Question 67. 51 ÷ _____ = – 51
Answer:
Solution:
The given equation is:
$51 \div \text{__________} = – 51$
We need to find the number that, when $51$ is divided by it, results in $-51$.
Let the missing number be $x$. The equation is:
$\frac{51}{x} = -51$
To find the value of $x$, we can multiply both sides of the equation by $x$ (assuming $x \neq 0$):
$\frac{51}{x} \times x = -51 \times x$
$51 = -51x$
Now, divide both sides of the equation by $-51$ (since $-51 \neq 0$):
$\frac{51}{-51} = \frac{-51x}{-51}$
$x = \frac{51}{-51}$
The division of a positive number by a negative number results in a negative number. The magnitudes are equal, so the division of magnitudes is 1.
$x = - ( \frac{51}{51} ) $
$x = -1$
Let's verify the solution by substituting $x = -1$ back into the original statement:
$51 \div (-1)$
When a positive integer is divided by $-1$, the result is its additive inverse.
$51 \div (-1) = -51$
This matches the given quotient.
Thus, the blank should be filled with $-1$.
The complete statement is 51 ÷ –1 = – 51.
The final answer is $-1$.
Question 68. 113 ÷ _____ = – 1
Answer:
Solution:
The given equation is:
$113 \div \text{__________} = – 1$
We need to find the number that, when $113$ is divided by it, results in $-1$.
Let the missing number be $x$. The equation is:
$\frac{113}{x} = -1$
To find the value of $x$, we can multiply both sides of the equation by $x$ (assuming $x \neq 0$):
$\frac{113}{x} \times x = -1 \times x$
$113 = -x$
To solve for $x$, we multiply both sides by $-1$:
$113 \times (-1) = -x \times (-1)$
$-113 = x$
So, $x = -113$.
Let's verify the solution by substituting $x = -113$ back into the original statement:
$113 \div (-113)$
When a positive integer is divided by a negative integer with the same absolute value, the result is $-1$.
$113 \div (-113) = - ( \frac{113}{113} ) = -1$
This matches the given quotient.
Thus, the blank should be filled with $-113$.
The complete statement is 113 ÷ –113 = – 1.
The final answer is $-113$.
Question 69. (– 95) ÷ _____ = 95
Answer:
Solution:
The given equation is:
$(-95) \div \text{__________} = 95$
We need to find the number that, when $-95$ is divided by it, results in $95$.
Let the missing number be $x$. The equation is:
$\frac{-95}{x} = 95$
To find the value of $x$, we can multiply both sides of the equation by $x$ (assuming $x \neq 0$):
$\frac{-95}{x} \times x = 95 \times x$
$-95 = 95x$
Now, divide both sides of the equation by $95$ (since $95 \neq 0$):
$\frac{-95}{95} = \frac{95x}{95}$
$x = \frac{-95}{95}$
The division of a negative number by a positive number results in a negative number. The magnitudes are equal, so the division of magnitudes is 1.
$x = - ( \frac{95}{95} ) $
$x = -1$
Let's verify the solution by substituting $x = -1$ back into the original statement:
$(-95) \div (-1)$
When a negative integer is divided by $-1$, the result is its additive inverse (positive value).
$(-95) \div (-1) = 95$
This matches the given quotient.
Thus, the blank should be filled with $-1$.
The complete statement is $(– 95) \div (– 1) = 95$.
The final answer is $-1$.
Question 70. (– 69) ÷ ( 69) = _____
Answer:
Solution:
The given expression is:
$(-69) \div ( 69) = \text{__________}$
We need to calculate the quotient when $-69$ is divided by $69$.
We are dividing a negative integer ($-69$) by a positive integer ($69$).
When a negative integer is divided by a positive integer, the quotient is a negative integer.
Negative $\div$ Positive = Negative
The magnitude of the quotient is obtained by dividing the absolute value of the dividend by the absolute value of the divisor.
$(-69) \div ( 69) = -( |{-69}| \div |69| )$
$|{-69}| = 69$
$|69| = 69$
Now, perform the division of the absolute values:
$69 \div 69 = 1$
Since the quotient is negative, we put a negative sign before the result:
$-(69 \div 69) = -1$
So, $(-69) \div ( 69) = -1$.
Thus, the blank should be filled with $-1$.
The complete statement is $(– 69) \div ( 69) = – 1$.
The final answer is $-1$.
Question 71. (– 28) ÷ ( – 28) = _____
Answer:
Solution:
The given expression is:
$(-28) \div ( – 28) = \text{__________}$
We need to calculate the quotient when $-28$ is divided by $-28$.
We are dividing a negative integer ($-28$) by another negative integer ($-28$).
When a negative integer is divided by a negative integer, the quotient is a positive integer.
Negative $\div$ Negative = Positive
The magnitude of the quotient is obtained by dividing the absolute value of the dividend by the absolute value of the divisor.
$(-28) \div (– 28) = |{-28}| \div |{-28}|$
$|{-28}| = 28$
Now, perform the division of the absolute values:
$28 \div 28 = 1$
Since the quotient is positive, the result is $1$.
So, $(-28) \div ( – 28) = 1$.
Note that any non-zero number divided by itself is equal to 1.
$\frac{a}{a} = 1$, for $a \neq 0$
Here, $a = -28$, which is non-zero.
Thus, the blank should be filled with $1$.
The complete statement is $(– 28) \div ( – 28) = 1$.
The final answer is $1$.
Question 72 to 108 (True or False)
In Questions 72 to 108, state whether the statements are True or False.
Question 72. 5 – (– 8) is same as 5 + 8.
Answer:
Solution:
The given statement is "5 – (– 8) is same as 5 + 8".
Let's evaluate the expression on the left side: $5 - (-8)$.
Subtracting a negative number is the same as adding its positive counterpart.
So, $5 - (-8) = 5 + 8$.
Now, let's evaluate the expression on the right side: $5 + 8$.
$5 + 8 = 13$.
Comparing the results, we have:
$5 - (-8) = 13$
$5 + 8 = 13$
Since both expressions evaluate to the same value (13), the statement is true.
The statement is True.
Question 73. (– 9) + (– 11) is greater than (– 9) – (– 11).
Answer:
Solution:
The given statement is "(– 9) + (– 11) is greater than (– 9) – (– 11)".
Let's evaluate the expression on the left side:
$(-9) + (-11)$
When adding two negative numbers, we add their absolute values and put a negative sign.
$(-9) + (-11) = -(9 + 11) = -20$
Let's evaluate the expression on the right side:
$(-9) - (-11)$
Subtracting a negative number is the same as adding its positive counterpart.
$(-9) - (-11) = (-9) + 11$
When adding a negative and a positive number, we find the difference between their absolute values and use the sign of the number with the larger absolute value.
$(-9) + 11 = 11 - 9 = 2$
Now, let's compare the two values:
$-20$ and $2$.
The statement claims that $(-9) + (-11)$ is greater than $(-9) - (-11)$, which means $-20 > 2$.
On the number line, $-20$ is to the left of $2$. Therefore, $-20$ is less than $2$.
So, the inequality $-20 > 2$ is false.
The statement is False.
Question 74. Sum of two negative integers always gives a number smaller than both the integers.
Answer:
Solution:
The given statement is "Sum of two negative integers always gives a number smaller than both the integers."
Let the two negative integers be $a$ and $b$, where $a < 0$ and $b < 0$.
Their sum is $a + b$.
Consider an example: Let $a = -5$ and $b = -3$.
The sum is $(-5) + (-3) = -8$.
We need to check if the sum (-8) is smaller than both original integers (-5 and -3).
Is $-8 < -5$? Yes.
Is $-8 < -3$? Yes.
This example supports the statement.
In general, when adding a negative number ($b < 0$) to another number ($a$), the result ($a+b$) is always smaller than the original number ($a$).
Similarly, when adding a negative number ($a < 0$) to another number ($b$), the result ($a+b$) is always smaller than the original number ($b$).
Thus, the sum of two negative integers is always smaller than each of the individual integers.
The statement is True.
Question 75. Difference of two negative integers cannot be a positive integer.
Answer:
Solution:
The given statement is "Difference of two negative integers cannot be a positive integer."
Let's consider the difference between two negative integers. Let the two negative integers be $a$ and $b$, where $a < 0$ and $b < 0$. The difference can be $a - b$ or $b - a$.
Let's choose two specific negative integers to test this statement.
Let the first negative integer be $-2$.
Let the second negative integer be $-5$.
Consider the difference between the first integer and the second integer: $(-2) - (-5)$.
Subtracting a negative number is equivalent to adding its positive counterpart.
$(-2) - (-5) = -2 + 5 = 3$
In this case, the difference is $3$, which is a positive integer.
This example shows that the difference of two negative integers *can* be a positive integer.
Therefore, the statement "Difference of two negative integers cannot be a positive integer" is false.
The statement is False.
Question 76. We can write a pair of integers whose sum is not an integer.
Answer:
Solution:
The given statement is "We can write a pair of integers whose sum is not an integer."
An integer is a whole number (positive, negative, or zero). Examples of integers are ..., -3, -2, -1, 0, 1, 2, 3, ...
One of the fundamental properties of integers is that they are **closed under addition**. This means that when you add any two integers, the result is always another integer.
Let $a$ and $b$ be any two integers.
Their sum is $a+b$. According to the property of integers, $a+b$ must be an integer.
Let's consider a few examples:
Example 1: Let the integers be 5 and -3.
Sum $= 5 + (-3) = 2$. The result $2$ is an integer.
Example 2: Let the integers be -10 and -4.
Sum $= (-10) + (-4) = -14$. The result $-14$ is an integer.
Example 3: Let the integers be 0 and 7.
Sum $= 0 + 7 = 7$. The result $7$ is an integer.
In all cases, the sum of two integers is an integer.
Therefore, it is not possible to find a pair of integers whose sum is not an integer.
The statement is False.
Question 77. Integers are closed under subtraction.
Answer:
Solution:
The given statement is "Integers are closed under subtraction."
For a set of numbers to be **closed under subtraction**, the difference between any two numbers from that set must also be a number in that same set.
The set of integers includes positive whole numbers, negative whole numbers, and zero {..., -3, -2, -1, 0, 1, 2, 3, ...}.
Let $a$ and $b$ be any two integers.
We need to check if the difference $a - b$ is always an integer.
Let's consider a few examples:
Example 1: Let $a = 5$ and $b = 3$. Both are integers.
$a - b = 5 - 3 = 2$. The result $2$ is an integer.
Example 2: Let $a = -8$ and $b = 2$. Both are integers.
$a - b = -8 - 2 = -10$. The result $-10$ is an integer.
Example 3: Let $a = 4$ and $b = -6$. Both are integers.
$a - b = 4 - (-6) = 4 + 6 = 10$. The result $10$ is an integer.
Example 4: Let $a = -7$ and $b = -3$. Both are integers.
$a - b = -7 - (-3) = -7 + 3 = -4$. The result $-4$ is an integer.
In all cases, the difference between two integers is always an integer.
Thus, the set of integers is closed under subtraction.
The statement is True.
Question 78. (– 23) + 47 is same as 47 + (– 23).
Answer:
Solution:
The given statement is "(– 23) + 47 is same as 47 + (– 23)".
This statement relates to the **commutative property of addition**, which states that for any two numbers $a$ and $b$, the order of addition does not affect the sum, i.e., $a + b = b + a$.
Let's evaluate the expression on the left side:
$(-23) + 47$
This is the sum of a negative integer and a positive integer. We find the difference between their absolute values ($|47| - |-23| = 47 - 23$) and use the sign of the integer with the larger absolute value (which is 47, a positive number).
$47 - 23 = 24$
So, $(-23) + 47 = 24$.
Now, let's evaluate the expression on the right side:
$47 + (-23)$
This is also the sum of a positive integer and a negative integer. Again, we find the difference between their absolute values ($|47| - |-23| = 47 - 23$) and use the sign of the integer with the larger absolute value (which is 47, a positive number).
$47 - 23 = 24$
So, $47 + (-23) = 24$.
Comparing the results:
$(-23) + 47 = 24$
$47 + (-23) = 24$
Since both sides evaluate to the same value (24), the statement is true.
The statement is True.
Question 79. When we change the order of integers, their sum remains the same.
Answer:
Solution:
The given statement is "When we change the order of integers, their sum remains the same."
This statement describes the **commutative property of addition** for integers.
The commutative property of addition states that for any two integers, say $a$ and $b$, their sum is the same regardless of the order in which they are added. Mathematically, this is expressed as:
$a + b = b + a$
Let's illustrate this with examples:
Example 1: Consider the integers 5 and -3.
Sum in original order: $5 + (-3) = 2$
Sum in changed order: $(-3) + 5 = 2$
The sum is 2 in both cases.
Example 2: Consider the integers -10 and -4.
Sum in original order: $(-10) + (-4) = -14$
Sum in changed order: $(-4) + (-10) = -14$
The sum is -14 in both cases.
Example 3: Consider the integers 0 and 7.
Sum in original order: $0 + 7 = 7$
Sum in changed order: $7 + 0 = 7$
The sum is 7 in both cases.
These examples and the commutative property of addition confirm that changing the order of integers does not change their sum.
The statement is True.
Question 80. When we change the order of integers their difference remains thesame.
Answer:
Solution:
The given statement is "When we change the order of integers their difference remains the same."
This statement is equivalent to asking if subtraction of integers is commutative.
For an operation to be commutative, the order of the operands does not affect the result. For subtraction, this would mean that for any two integers $a$ and $b$, $a - b$ must be equal to $b - a$.
Let's test this with an example using two integers.
Let the integers be $a = 7$ and $b = 4$. Both 7 and 4 are integers.
Calculate the difference $a - b$:
$7 - 4 = 3$
Now, change the order and calculate the difference $b - a$:
$4 - 7 = -3$
Comparing the results, $3$ and $-3$, we see that $3 \neq -3$.
Since we found an example where changing the order of the integers changes their difference, subtraction of integers is not commutative.
Therefore, the statement "When we change the order of integers their difference remains the same" is false.
The statement is False.
Question 81. Going 500 m towards east first and then 200 m back is same as going 200 m towards west first and then going 500 m back.
Answer:
Solution:
The given statement compares two sequences of movements.
Let's represent movement towards East as a positive value and movement towards West as a negative value.
Consider the first scenario: "Going 500 m towards east first and then 200 m back".
Going 500 m towards East is represented as $+500$ m.
Going 200 m back means going 200 m towards the West, which is represented as $-200$ m.
The net displacement from the starting point in this scenario is the sum of these movements:
$500 + (-200) = 500 - 200 = 300$ m.
This means the final position is 300 m towards the East from the starting point.
Consider the second scenario: "going 200 m towards west first and then going 500 m back".
Going 200 m towards West is represented as $-200$ m.
Going 500 m back means going 500 m towards the East, which is represented as $+500$ m.
The net displacement from the starting point in this scenario is the sum of these movements:
$(-200) + 500 = 500 - 200 = 300$ m.
This means the final position is 300 m towards the East from the starting point.
Comparing the net displacements of the two scenarios, we find they are both 300 m towards the East.
Since the final position relative to the starting point is the same in both cases, the two scenarios are equivalent in terms of net displacement.
The statement is True.
Question 82. (– 5) × (33) = 5 × ( – 33)
Answer:
Solution:
The given statement is "$(-5) \times (33) = 5 \times (-33)$".
Let's evaluate the expression on the left side:
$(-5) \times (33)$
When a negative integer is multiplied by a positive integer, the product is a negative integer.
$5 \times 33 = 165$
So, $(-5) \times 33 = -165$.
Now, let's evaluate the expression on the right side:
$5 \times (-33)$
When a positive integer is multiplied by a negative integer, the product is a negative integer.
$5 \times 33 = 165$
So, $5 \times (-33) = -165$.
Comparing the results:
Left side: $-165$
Right side: $-165$
Since $-165 = -165$, the statement is true.
The statement is True.
Question 83. (– 19) × (– 11) = 19 × 11
Answer:
Solution:
The given statement is "$(-19) \times (-11) = 19 \times 11$".
Let's evaluate the expression on the left side:
$(-19) \times (-11)$
When two negative integers are multiplied, the product is a positive integer.
$(-19) \times (-11) = 19 \times 11$
$19 \times 11 = 209$
So, $(-19) \times (-11) = 209$.
Now, let's evaluate the expression on the right side:
$19 \times 11$
This is the product of two positive integers, which is a positive integer.
$19 \times 11 = 209$
So, $19 \times 11 = 209$.
Comparing the results:
Left side: $209$
Right side: $209$
Since $209 = 209$, the statement is true.
The statement is True.
Question 84. (– 20) × ( 5 – 3) = (– 20) × ( – 2)
Answer:
Solution:
The given statement is "$(-20) \times ( 5 – 3) = (-20) \times ( – 2)$".
Let's evaluate the expression on the left side (LHS):
LHS $= (-20) \times (5 - 3)$
First, perform the operation inside the parentheses:
$5 - 3 = 2$
Now, substitute this back into the expression:
LHS $= (-20) \times 2$
Multiply the negative integer by the positive integer:
LHS $= -40$
Now, let's evaluate the expression on the right side (RHS):
RHS $= (-20) \times (-2)$
Multiply the two negative integers. The product of two negative integers is a positive integer.
RHS $= 20 \times 2$
RHS $= 40$
Now, let's compare the results of the LHS and RHS:
LHS $= -40$
RHS $= 40$
Is $-40$ equal to $40$? No, $-40 \neq 40$.
Since the left side is not equal to the right side, the statement is false.
The statement is False.
Question 85. 4 × (– 5) = (– 10) × (– 2)
Answer:
Solution:
The given statement is "$4 \times (– 5) = (– 10) \times (– 2)$".
Let's evaluate the expression on the left side (LHS):
LHS $= 4 \times (-5)$
When a positive integer is multiplied by a negative integer, the product is a negative integer.
LHS $= -(4 \times 5)$
LHS $= -20$
Now, let's evaluate the expression on the right side (RHS):
RHS $= (-10) \times (-2)$
When two negative integers are multiplied, the product is a positive integer.
RHS $= 10 \times 2$
RHS $= 20$
Now, let's compare the results of the LHS and RHS:
LHS $= -20$
RHS $= 20$
Is $-20$ equal to $20$? No, $-20 \neq 20$.
Since the left side is not equal to the right side, the statement is false.
The statement is False.
Question 86. (– 1) × (– 2) × (– 3) = 1 × 2 × 3
Answer:
Solution:
The given statement is "$(- 1) \times (– 2) \times (– 3) = 1 \times 2 \times 3$".
Let's evaluate the expression on the left side (LHS):
LHS $= (-1) \times (-2) \times (-3)$
First, multiply the first two numbers:
$(-1) \times (-2) = +2$ (The product of two negative integers is positive).
Now, multiply the result by the third number:
$+2 \times (-3) = -6$ (The product of a positive integer and a negative integer is negative).
So, LHS $= -6$.
Now, let's evaluate the expression on the right side (RHS):
RHS $= 1 \times 2 \times 3$
Multiply the numbers:
$1 \times 2 = 2$
$2 \times 3 = 6$
So, RHS $= 6$.
Now, let's compare the results of the LHS and RHS:
LHS $= -6$
RHS $= 6$
Is $-6$ equal to $6$? No, $-6 \neq 6$.
Since the left side is not equal to the right side, the statement is false.
The statement is False.
Question 87. – 3 × 3 = – 12 – ( – 3)
Answer:
Solution:
The given statement is "– 3 × 3 = – 12 – ( – 3)".
Let's evaluate the expression on the left side (LHS):
LHS $= -3 \times 3$
When a negative integer is multiplied by a positive integer, the product is negative.
LHS $= -(3 \times 3)$
LHS $= -9$
Now, let's evaluate the expression on the right side (RHS):
RHS $= -12 - (-3)$
Subtracting a negative number is the same as adding its positive counterpart.
RHS $= -12 + 3$
When adding a negative integer and a positive integer, we find the difference between their absolute values ($|-12| - |3| = 12 - 3 = 9$) and use the sign of the integer with the larger absolute value (which is $-12$).
RHS $= -9$
Now, let's compare the results of the LHS and RHS:
LHS $= -9$
RHS $= -9$
Since $-9 = -9$, the statement is true.
The statement is True.
Question 88. Product of two negative integers is a negative integer.
Answer:
Solution:
The given statement is "Product of two negative integers is a negative integer."
Let's consider the rules for multiplying integers:
- Positive integer $\times$ Positive integer $=$ Positive integer
- Negative integer $\times$ Negative integer $=$ Positive integer
- Positive integer $\times$ Negative integer $=$ Negative integer
- Negative integer $\times$ Positive integer $=$ Negative integer
According to the rules, the product of two negative integers is always a **positive** integer.
Let's consider an example:
Let the two negative integers be $-4$ and $-5$.
Their product is $(-4) \times (-5)$.
$(-4) \times (-5) = 20$.
The result $20$ is a positive integer, not a negative integer.
Since the product of two negative integers is a positive integer, the statement is false.
The statement is False.
Question 89. Product of three negative integers is a negative integer.
Answer:
Solution:
The given statement is "Product of three negative integers is a negative integer."
Let's consider the rules for multiplying integers based on their signs:
- Product of two positive integers is positive.
- Product of two negative integers is positive.
- Product of a positive integer and a negative integer (in any order) is negative.
We need to find the sign of the product of three negative integers. Let the three negative integers be $a$, $b$, and $c$, where $a < 0$, $b < 0$, and $c < 0$.
We can find the product step by step:
First, consider the product of the first two negative integers, $a \times b$.
According to the rules, the product of two negative integers is a positive integer. So, $a \times b > 0$.
Next, multiply this positive result $(a \times b)$ by the third negative integer $c$.
We are multiplying a positive integer by a negative integer: $(a \times b) \times c$.
According to the rules, the product of a positive integer and a negative integer is a negative integer. So, $(a \times b) \times c < 0$.
Let's verify with an example:
Consider the three negative integers $-2$, $-3$, and $-4$.
Product $= (-2) \times (-3) \times (-4)$
First, $(-2) \times (-3) = 6$ (positive)
Then, $6 \times (-4) = -24$ (negative)
The result, $-24$, is a negative integer.
This confirms that the product of three negative integers is a negative integer.
The statement is True.
Question 90. Product of a negative integer and a positive integer is a positive integer.
Answer:
Solution:
The given statement is "Product of a negative integer and a positive integer is a positive integer."
Let's examine the rule for the product of integers with different signs.
When a negative integer is multiplied by a positive integer, the result is always a negative integer.
Similarly, when a positive integer is multiplied by a negative integer, the result is always a negative integer.
Let's consider an example to verify the statement.
Let the negative integer be $-6$.
Let the positive integer be $4$.
Calculate their product: $(-6) \times 4$.
$(-6) \times 4 = -24$.
The result, $-24$, is a negative integer.
Since the product of a negative integer and a positive integer results in a negative integer (as shown by the example and the general rule), the statement that the product is a positive integer is false.
The statement is False.
Question 91. When we multiply two integers their product is always greater than both the integers.
Answer:
Solution:
The given statement is "When we multiply two integers their product is always greater than both the integers."
This statement claims that for any two integers $a$ and $b$, their product $a \times b$ will satisfy the conditions $a \times b > a$ and $a \times b > b$.
To check if this statement is true for *all* integers, we can try some examples.
Example 1: Let the integers be $a = 5$ and $b = 1$. Both are integers.
Their product is $5 \times 1 = 5$.
Is the product (5) greater than both integers (5 and 1)?
Is $5 > 5$? This is false.
Is $5 > 1$? This is true.
Since the first condition ($5 > 5$) is false, the product is not greater than both integers in this case.
Example 2: Let the integers be $a = 2$ and $b = 0$. Both are integers.
Their product is $2 \times 0 = 0$.
Is the product (0) greater than both integers (2 and 0)?
Is $0 > 2$? This is false.
Is $0 > 0$? This is false.
The product is not greater than either integer in this case.
Example 3: Let the integers be $a = -2$ and $b = 3$. Both are integers.
Their product is $(-2) \times 3 = -6$.
Is the product (-6) greater than both integers (-2 and 3)?
Is $-6 > -2$? This is false (since -6 is to the left of -2 on the number line).
Is $-6 > 3$? This is false.
The product is smaller than both integers in this case.
Since we have found examples where the product of two integers is not greater than both of the integers (it can be equal to one, smaller than one, or smaller than both), the statement is false.
The statement is False.
Question 92. Integers are closed under multiplication.
Answer:
Solution:
The given statement is "Integers are closed under multiplication."
For a set of numbers to be **closed under multiplication**, the product of any two numbers from that set must also be a number in that same set.
The set of integers ($\mathbb{Z}$) consists of positive whole numbers, negative whole numbers, and zero: {..., -3, -2, -1, 0, 1, 2, 3, ...}.
Let $a$ and $b$ be any two integers.
We need to determine if their product $a \times b$ is always an integer.
Let's consider various cases:
Case 1: Both integers are positive.
Example: $4 \times 5 = 20$. $4, 5,$ and $20$ are integers.
Case 2: Both integers are negative.
Example: $(-6) \times (-3) = 18$. $-6, -3,$ and $18$ are integers.
Case 3: One integer is positive and the other is negative.
Example: $7 \times (-2) = -14$. $7, -2,$ and $-14$ are integers.
Case 4: One or both integers are zero.
Example: $5 \times 0 = 0$. $5, 0,$ and $0$ are integers.
Example: $(-9) \times 0 = 0$. $-9, 0,$ and $0$ are integers.
In all these cases, the product of two integers is found to be an integer.
This property holds true for all pairs of integers.
Therefore, the set of integers is closed under multiplication.
The statement is True.
Question 93. (–237) × 0 is same as 0 × (–39)
Answer:
Solution:
The given statement is "$(-237) \times 0$ is same as $0 \times (–39)$".
Let's evaluate the expression on the left side (LHS):
LHS $= (-237) \times 0$
According to the property of multiplication by zero, the product of any integer and zero is always zero.
LHS $= 0$
Now, let's evaluate the expression on the right side (RHS):
RHS $= 0 \times (-39)$
Again, the product of zero and any integer is always zero.
RHS $= 0$
Now, let's compare the results of the LHS and RHS:
LHS $= 0$
RHS $= 0$
Since $0 = 0$, the left side is equal to the right side.
Therefore, the statement is true.
The statement is True.
Question 94. Multiplication is not commutative for integers.
Answer:
Solution:
The given statement is "Multiplication is not commutative for integers."
For an operation to be **commutative**, the order of the operands does not affect the result. In the context of multiplication, this means that for any two integers $a$ and $b$, the product $a \times b$ must be equal to the product $b \times a$. Mathematically, the commutative property of multiplication is expressed as:
$a \times b = b \times a$
Let's test this property with some examples of integers:
Example 1: Let $a = 5$ and $b = 3$. Both are integers.
$a \times b = 5 \times 3 = 15$
$b \times a = 3 \times 5 = 15$
Here, $5 \times 3 = 3 \times 5$.
Example 2: Let $a = -4$ and $b = 6$. Both are integers.
$a \times b = (-4) \times 6 = -24$
$b \times a = 6 \times (-4) = -24$
Here, $(-4) \times 6 = 6 \times (-4)$.
Example 3: Let $a = -7$ and $b = -2$. Both are integers.
$a \times b = (-7) \times (-2) = 14$
$b \times a = (-2) \times (-7) = 14$
Here, $(-7) \times (-2) = (-2) \times (-7)$.
Example 4: Let $a = 9$ and $b = 0$. Both are integers.
$a \times b = 9 \times 0 = 0$
$b \times a = 0 \times 9 = 0$
Here, $9 \times 0 = 0 \times 9$.
In all the examples, changing the order of the integers does not change the product.
The commutative property of multiplication ($a \times b = b \times a$) holds true for all integers.
Therefore, multiplication **is** commutative for integers.
The statement "Multiplication is not commutative for integers" contradicts this property.
The statement is False.
Question 95. (–1) is not a multiplicative identity of integers.
Answer:
Solution:
The given statement is "–1 is not a multiplicative identity of integers."
A **multiplicative identity** for a set of numbers is a number, usually denoted by $e$, such that for any number $a$ in the set, the product of $a$ and $e$ is $a$ itself. That is, $a \times e = a$ and $e \times a = a$.
For the set of integers, the multiplicative identity is the number that leaves any integer unchanged when multiplied by it.
Let's consider the number 1.
For any integer $a$, we know that:
$a \times 1 = a$
And
$1 \times a = a$
Thus, 1 is the multiplicative identity for integers.
Now let's consider the number -1, as mentioned in the statement.
For -1 to be the multiplicative identity, it must satisfy the condition that for any integer $a$, $a \times (-1) = a$ and $(-1) \times a = a$.
Let's test this with an arbitrary integer, say $a = 5$.
$5 \times (-1) = -5$
In this case, $-5$ is not equal to $5$.
Let's test with another integer, say $a = -10$.
$(-10) \times (-1) = 10$
In this case, $10$ is not equal to $-10$.
The only integer for which $a \times (-1) = a$ holds true is $a=0$ ($0 \times (-1) = 0$), but the property must hold for *all* integers.
Since multiplying an integer by -1 does not result in the same integer (except for 0), -1 is not the multiplicative identity of integers.
The statement "–1 is not a multiplicative identity of integers" is therefore true.
The statement is True.
Question 96. 99 × 101 can be written as (100 – 1) × (100 + 1)
Answer:
Solution:
The given statement is "99 × 101 can be written as (100 – 1) × (100 + 1)".
Let's evaluate the expression on the left side (LHS):
LHS $= 99 \times 101$
To calculate this product, we can multiply 99 by 100 and then add 99 (since $101 = 100 + 1$):
$99 \times 101 = 99 \times (100 + 1) = (99 \times 100) + (99 \times 1) = 9900 + 99 = 9999$.
So, LHS $= 9999$.
Now, let's evaluate the expression on the right side (RHS):
RHS $= (100 – 1) \times (100 + 1)$
First, evaluate the terms inside the parentheses:
$100 - 1 = 99$
$100 + 1 = 101$
Now, substitute these values back into the expression:
RHS $= 99 \times 101$
RHS $= 9999$ (from the LHS calculation).
Alternatively, we can use the algebraic identity $(a - b)(a + b) = a^2 - b^2$. Here, $a = 100$ and $b = 1$.
RHS $= (100 - 1) \times (100 + 1) = 100^2 - 1^2$
$100^2 = 100 \times 100 = 10000$
$1^2 = 1 \times 1 = 1$
RHS $= 10000 - 1 = 9999$
Comparing the results of the LHS and RHS:
LHS $= 9999$
RHS $= 9999$
Since $9999 = 9999$, the left side is equal to the right side.
Thus, $99 \times 101$ can indeed be written as $(100 – 1) \times (100 + 1)$.
The statement is True.
Question 97. If a, b, c are integers and b ≠ 0 then, a × (b – c) = a × b – a × c
Answer:
Solution:
The given statement is "If a, b, c are integers and b ≠ 0 then, $a \times (b – c) = a \times b – a \times c$".
The equality $a \times (b – c) = a \times b – a \times c$ represents the **distributive property of multiplication over subtraction** for integers.
This property states that for any three integers $a$, $b$, and $c$, multiplying $a$ by the difference of $b$ and $c$ gives the same result as multiplying $a$ by $b$ and then subtracting the product of $a$ and $c$.
Mathematically, this property is written as:
$a \times (b - c) = (a \times b) - (a \times c)$
Let's test this property with some examples using integers, including cases where $b \neq 0$ as specified in the statement.
Example 1: Let $a = 5$, $b = 8$, $c = 3$. Here $b=8 \neq 0$.
LHS = $a \times (b - c) = 5 \times (8 - 3) = 5 \times 5 = 25$.
RHS = $(a \times b) - (a \times c) = (5 \times 8) - (5 \times 3) = 40 - 15 = 25$.
LHS = RHS.
Example 2: Let $a = -2$, $b = 6$, $c = 10$. Here $b=6 \neq 0$.
LHS = $a \times (b - c) = (-2) \times (6 - 10) = (-2) \times (-4) = 8$.
RHS = $(a \times b) - (a \times c) = ((-2) \times 6) - ((-2) \times 10) = (-12) - (-20) = -12 + 20 = 8$.
LHS = RHS.
Example 3: Let $a = 3$, $b = -4$, $c = -7$. Here $b=-4 \neq 0$.
LHS = $a \times (b - c) = 3 \times ((-4) - (-7)) = 3 \times (-4 + 7) = 3 \times 3 = 9$.
RHS = $(a \times b) - (a \times c) = (3 \times (-4)) - (3 \times (-7)) = (-12) - (-21) = -12 + 21 = 9$.
LHS = RHS.
The distributive property of multiplication over subtraction, $a \times (b - c) = a \times b - a \times c$, is a fundamental property that holds true for all integers $a$, $b$, and $c$. The additional condition $b \neq 0$ does not make the statement false; the equality holds regardless of whether $b$ is zero or not.
Thus, the statement is true.
The statement is True.
Question 98. (a + b) × c = a × c + a × b
Answer:
Solution:
The given statement is "$(a + b) \times c = a \times c + a \times b$".
This statement involves the operations of addition and multiplication of integers.
Let's evaluate the left side (LHS) and the right side (RHS) of the equality using some arbitrary integer values for $a$, $b$, and $c$.
Let $a = 2$, $b = 3$, and $c = 4$. All are integers.
Evaluate the LHS: $(a + b) \times c$
LHS $= (2 + 3) \times 4$
LHS $= 5 \times 4$
LHS $= 20$
Evaluate the RHS: $a \times c + a \times b$
RHS $= (2 \times 4) + (2 \times 3)$
RHS $= 8 + 6$
RHS $= 14$
Now, let's compare the results of the LHS and RHS:
LHS $= 20$
RHS $= 14$
Is $20$ equal to $14$? No, $20 \neq 14$.
The statement would be true if it represented the distributive property of multiplication over addition, which is $(a + b) \times c = a \times c + b \times c$ or $c \times (a + b) = c \times a + c \times b$. The given statement has $a \times b$ on the RHS instead of $b \times c$.
Since we found a case where the equality does not hold, the statement is false.
The statement is False.
Question 99. a × b = b × a
Answer:
Solution:
The given statement is "$a \times b = b \times a$".
This statement describes the **commutative property of multiplication**.
The commutative property of multiplication states that for any two numbers (in this context, integers), the order in which they are multiplied does not change the result of the multiplication (the product).
In other words, if $a$ and $b$ are integers, then the product of $a$ and $b$ is the same as the product of $b$ and $a$.
Let's verify this with a couple of examples using integers:
Example 1: Let $a = 6$ and $b = 4$. Both are integers.
$a \times b = 6 \times 4 = 24$
$b \times a = 4 \times 6 = 24$
In this case, $6 \times 4 = 4 \times 6$, so the equality holds.
Example 2: Let $a = -5$ and $b = 7$. Both are integers.
$a \times b = (-5) \times 7 = -35$
$b \times a = 7 \times (-5) = -35$
In this case, $(-5) \times 7 = 7 \times (-5)$, so the equality holds.
Example 3: Let $a = -3$ and $b = -8$. Both are integers.
$a \times b = (-3) \times (-8) = 24$
$b \times a = (-8) \times (-3) = 24$
In this case, $(-3) \times (-8) = (-8) \times (-3)$, so the equality holds.
The commutative property of multiplication holds true for all pairs of integers.
Therefore, the statement $a \times b = b \times a$ is true for integers.
The statement is True.
Question 100. a ÷ b = b ÷ a
Answer:
Solution:
The given statement is "$a \div b = b \div a$".
This statement tests whether division is **commutative** for integers.
For an operation to be commutative, changing the order of the numbers involved does not change the result.
For division to be commutative, for any two integers $a$ and $b$ (where $b \neq 0$ and $a \neq 0$ to avoid division by zero and trivial cases like $0 \div 0$), the result of $a \div b$ must be equal to the result of $b \div a$.
Let's consider an example using two different non-zero integers.
Let $a = 10$ and $b = 5$. Both are integers, and both are non-zero.
Calculate $a \div b$:
$a \div b = 10 \div 5 = 2$
Now, change the order and calculate $b \div a$:
$b \div a = 5 \div 10 = \frac{5}{10} = \frac{1}{2}$
Comparing the results, $2$ and $\frac{1}{2}$, we see that $2 \neq \frac{1}{2}$.
Since we found a pair of integers where $a \div b$ is not equal to $b \div a$, division is not commutative for integers.
Therefore, the statement $a \div b = b \div a$ is false for integers in general.
The statement is False.
Question 101. a – b = b – a
Answer:
Solution:
The given statement is "$a – b = b – a$".
This statement is asking whether subtraction of integers is **commutative**.
For an operation to be commutative, changing the order of the operands does not change the result.
For subtraction, this would mean that for any two integers $a$ and $b$, the difference $a - b$ must be equal to the difference $b - a$.
Let's test this with an example using two different integers.
Let $a = 5$ and $b = 2$. Both 5 and 2 are integers.
Calculate $a - b$:
$a - b = 5 - 2 = 3$
Now, change the order and calculate $b - a$:
$b - a = 2 - 5 = -3$
Comparing the results, $3$ and $-3$, we see that $3 \neq -3$.
Since we found a pair of integers where $a - b$ is not equal to $b - a$, subtraction is not commutative for integers.
The only case where $a - b = b - a$ is when $a-b - (b-a) = 0 \implies a-b-b+a = 0 \implies 2a-2b = 0 \implies 2(a-b) = 0 \implies a-b = 0 \implies a=b$. The statement is only true if $a$ and $b$ are the same integer, but it is not true for all pairs of integers.
Therefore, the statement $a – b = b – a$ is generally false for integers.
The statement is False.
Question 102. a ÷ (–b) = – (a ÷ b)
Answer:
Solution:
The given statement is "$a \div (–b) = – (a \div b)$".
We need to determine if this equality holds true for integers $a$ and $b$, assuming $b \neq 0$ since division by zero is undefined.
Let's evaluate the expression on the left side (LHS):
LHS $= a \div (-b)$
Using fraction notation, this can be written as $\frac{a}{-b}$.
A property of fractions states that $\frac{a}{-b} = -\frac{a}{b}$ for any integers $a$ and $b$ where $b \neq 0$.
So, LHS $= -\frac{a}{b}$.
Now, let's evaluate the expression on the right side (RHS):
RHS $= – (a \div b)$
Using fraction notation, $a \div b = \frac{a}{b}$.
So, RHS $= - \left(\frac{a}{b}\right) = -\frac{a}{b}$.
Comparing the results of the LHS and RHS:
LHS $= -\frac{a}{b}$
RHS $= -\frac{a}{b}$
Since LHS = RHS, the statement $a \div (–b) = – (a \div b)$ is true for all integers $a$ and all non-zero integers $b$.
Let's confirm with an example:
Let $a = 12$ and $b = 3$.
LHS $= 12 \div (-3) = -4$.
RHS $= -(12 \div 3) = -(4) = -4$.
LHS = RHS.
Let $a = -15$ and $b = 5$.
LHS $= (-15) \div (-5) = 3$.
RHS $= -((-15) \div 5) = -(-3) = 3$.
LHS = RHS.
Let $a = 20$ and $b = -4$.
LHS $= 20 \div (-(-4)) = 20 \div 4 = 5$.
RHS $= -(20 \div (-4)) = -(-5) = 5$.
LHS = RHS.
Let $a = -24$ and $b = -6$.
LHS $= (-24) \div (-(-6)) = (-24) \div 6 = -4$.
RHS $= -((-24) \div (-6)) = -(4) = -4$.
LHS = RHS.
The equality holds true in all cases (where $b \neq 0$).
The statement is True.
Question 103. a ÷ ( –1) = – a
Answer:
Solution:
The given statement is "$a \div (–1) = – a$".
We need to determine if this equality holds true for any integer $a$.
Let's evaluate the expression on the left side (LHS):
LHS $= a \div (-1)$
Dividing any number by -1 gives the number with the opposite sign.
Using fraction notation, this is $\frac{a}{-1}$.
For any integer $a$, $\frac{a}{-1} = -a$.
So, LHS $= -a$.
Now, let's consider the expression on the right side (RHS):
RHS $= -a$
The expression $-a$ represents the opposite (or additive inverse) of the integer $a$.
Comparing the results of the LHS and RHS:
LHS $= -a$
RHS $= -a$
Since LHS = RHS, the statement $a \div (–1) = – a$ is true for all integers $a$.
Let's confirm with examples:
Example 1: Let $a = 5$.
LHS $= 5 \div (-1) = -5$.
RHS $= -5$.
LHS = RHS.
Example 2: Let $a = -10$.
LHS $= (-10) \div (-1) = 10$.
RHS $= -(-10) = 10$.
LHS = RHS.
Example 3: Let $a = 0$.
LHS $= 0 \div (-1) = 0$.
RHS $= -0 = 0$.
LHS = RHS.
The equality holds true for all integers $a$.
The statement is True.
Question 104. Multiplication fact (–8) × (–10) = 80 is same as division fact 80 ÷ (– 8) = (–10)
Answer:
Solution:
The given statement is "Multiplication fact $(–8) \times (–10) = 80$ is same as division fact $80 \div (– 8) = (–10)$".
First, let's verify the multiplication fact:
$(–8) \times (–10)$
The product of two negative integers is a positive integer.
$(-8) \times (-10) = +(8 \times 10) = 80$.
So, the multiplication fact $(–8) \times (–10) = 80$ is correct.
Next, let's verify the division fact:
$80 \div (– 8)$
When a positive integer is divided by a negative integer, the quotient is a negative integer.
$80 \div (-8) = -(80 \div 8) = -10$.
So, the division fact $80 \div (– 8) = (–10)$ is correct.
Multiplication and division are inverse operations. If $a \times b = c$ (where $b \neq 0$), then it implies $c \div b = a$. Similarly, if $a \times b = c$ (where $a \neq 0$), then it implies $c \div a = b$.
In the given multiplication fact, let $a = -8$, $b = -10$, and $c = 80$.
$(–8) \times (–10) = 80$
If we divide the product ($c=80$) by one of the factors ($a=-8$), we should get the other factor ($b=-10$).
$80 \div (-8)$ should equal $-10$.
As we calculated above, $80 \div (-8) = -10$. This matches the given division fact.
Since the division fact $80 \div (– 8) = (–10)$ is a valid division statement derived from the multiplication fact $(–8) \times (–10) = 80$ using the inverse relationship, the statement is true.
The statement is True.
Question 105. Integers are closed under division.
Answer:
Solution:
The given statement is "Integers are closed under division."
For a set of numbers to be **closed under division**, the result of dividing any number from that set by any other non-zero number from that set must also be a number in that same set.
The set of integers consists of positive whole numbers, negative whole numbers, and zero: {..., -3, -2, -1, 0, 1, 2, 3, ...}.
Division by zero is undefined, so we only consider division by non-zero integers.
Let's test the closure property with some examples using non-zero integers.
Example 1: Let $a = 10$ and $b = 2$. Both are integers, and $b \neq 0$.
The result of $a \div b$ is $10 \div 2 = 5$. The result $5$ is an integer.
This example supports the statement.
Example 2: Let $a = 5$ and $b = 2$. Both are integers, and $b \neq 0$.
The result of $a \div b$ is $5 \div 2 = \frac{5}{2}$.
Is the result $\frac{5}{2}$ an integer? No, $\frac{5}{2} = 2.5$, which is a rational number but not an integer.
Since we found a pair of integers (5 and 2) such that their division results in a number ($\frac{5}{2}$) that is not an integer, the set of integers is not closed under division.
Therefore, the statement "Integers are closed under division" is false.
The statement is False.
Question 106. [(–32) ÷ 8 ] ÷ 2 = –32 ÷ [ 8 ÷ 2]
Answer:
Solution:
The given statement is "$[(–32) \div 8 ] \div 2 = –32 \div [ 8 \div 2]$".
This statement tests the associative property of division for integers. For division to be associative, for any three integers $a$, $b$, and $c$ (with $b \neq 0$ and $c \neq 0$, and $[b \div c] \neq 0$ for the RHS), the equality $(a \div b) \div c = a \div (b \div c)$ must hold.
Let's evaluate the expression on the left side (LHS):
LHS $= [(-32) \div 8 ] \div 2$
First, calculate the expression inside the parentheses:
$(-32) \div 8 = -4$ (since a negative number divided by a positive number is negative, and $32 \div 8 = 4$).
Now, substitute this result back into the LHS expression:
LHS $= -4 \div 2$
Divide the negative integer by the positive integer:
LHS $= -2$ (since a negative number divided by a positive number is negative, and $4 \div 2 = 2$).
Now, let's evaluate the expression on the right side (RHS):
RHS $= -32 \div [ 8 \div 2]$
First, calculate the expression inside the brackets:
$8 \div 2 = 4$ (since a positive number divided by a positive number is positive, and $8 \div 2 = 4$).
Now, substitute this result back into the RHS expression:
RHS $= -32 \div 4$
Divide the negative integer by the positive integer:
RHS $= -8$ (since a negative number divided by a positive number is negative, and $32 \div 4 = 8$).
Comparing the results of the LHS and RHS:
LHS $= -2$
RHS $= -8$
Is $-2$ equal to $-8$? No, $-2 \neq -8$.
Since the left side is not equal to the right side, the statement is false. This demonstrates that division is not associative for integers.
The statement is False.
Question 107. The sum of an integer and its additive inverse is zero (0).
Answer:
Solution:
The given statement is "The sum of an integer and its additive inverse is zero (0)."
The **additive inverse** of an integer $a$ is the integer $-a$. The property of additive inverses is that when an integer is added to its additive inverse, the result is the additive identity, which is 0.
So, for any integer $a$, its additive inverse is $-a$.
The statement claims that the sum of $a$ and $-a$ is 0.
$a + (-a) = 0$
Also, $(-a) + a = 0$.
Let's verify this with examples:
Example 1: Let the integer be 7.
The additive inverse of 7 is -7.
The sum is $7 + (-7) = 0$.
Example 2: Let the integer be -15.
The additive inverse of -15 is $-(-15) = 15$.
The sum is $(-15) + 15 = 0$.
Example 3: Let the integer be 0.
The additive inverse of 0 is $-0 = 0$.
The sum is $0 + 0 = 0$.
In all cases, the sum of an integer and its additive inverse is 0.
This property is a fundamental definition of the additive inverse in the set of integers.
The statement is True.
Question 108. The successor of 0 × (–25) is 1 × (–25)
Answer:
Solution:
The given statement is "The successor of $0 \times (–25)$ is $1 \times (–25)$".
Let's evaluate the expressions involved in the statement.
First, consider the expression $0 \times (–25)$.
The product of any number and zero is always zero.
$0 \times (-25) = 0$
Now, we need to find the successor of this result (which is 0).
The successor of an integer is obtained by adding 1 to the integer.
The successor of 0 is $0 + 1 = 1$.
So, the first part of the statement, "The successor of $0 \times (–25)$", evaluates to 1.
Next, consider the expression $1 \times (–25)$.
The product of 1 and any integer is the integer itself (1 is the multiplicative identity).
$1 \times (-25) = -25$
So, the second part of the statement, "$1 \times (–25)$", evaluates to -25.
Now, we compare the results of the two parts. The statement claims that the successor of $0 \times (–25)$ is equal to $1 \times (–25)$.
We found that the successor of $0 \times (–25)$ is 1.
We found that $1 \times (–25)$ is -25.
Is $1$ equal to $-25$? No, $1 \neq -25$.
Since the two values are not equal, the given statement is false.
The statement is False.
Question 109 to 136
Question 109. Observe the following patterns and fill in the blanks to make the statements true:
(a) – 5 × 4 = – 20
– 5 × 3 = – 15 = –20 – ( – 5)
– 5 × 2 = _______ = – 15 – ( –5)
– 5 × 1 = _______ = _______
– 5 × 0 = 0 = _______
– 5 × – 1 = 5 = _______
– 5 × – 2 = _______ = _______
(b) 7 × 4 = 28
7 × 3 = _______ = 28 – 7
7 × 2 = __ __ = _______– 7
7 × 1 = 7 = _______ – 7
7 × 0 = _______ = _______ –________
7 × – 1 = –7 = _______ – _______
7 × – 2 = _______ = _______ – _______
7 × – 3 _______ = _______ – ________
Answer:
Solution:
We need to observe the pattern in the given multiplication and subtraction expressions and fill in the blanks.
(a) The pattern on the left side is $-5$ multiplied by a decreasing integer. The pattern on the right side is the previous result minus $(-5)$, which is equivalent to adding 5.
– 5 × 4 = – 20
– 5 × 3 = – 15 = –20 – ( – 5)
– 5 × 2 = – 10 = – 15 – ( –5) (Since $-15 - (-5) = -15 + 5 = -10$)
– 5 × 1 = – 5 = – 10 – ( –5) (Since $-5 = -10 - (-5) = -10 + 5 = -5$)
– 5 × 0 = 0 = – 5 – ( –5) (Since $0 = -5 - (-5) = -5 + 5 = 0$)
– 5 × – 1 = 5 = 0 – ( –5) (Since $5 = 0 - (-5) = 0 + 5 = 5$)
– 5 × – 2 = 10 = 5 – ( –5) (Since $(-5) \times (-2) = 10$ and $10 = 5 - (-5) = 5 + 5 = 10$)
(b) The pattern on the left side is $7$ multiplied by a decreasing integer. The pattern on the right side is the previous result minus $7$.
7 × 4 = 28
7 × 3 = 21 = 28 – 7 (Since $7 \times 3 = 21$ and $28 - 7 = 21$)
7 × 2 = 14 = 21 – 7 (Since $7 \times 2 = 14$ and $21 - 7 = 14$)
7 × 1 = 7 = 14 – 7 (Since $7 \times 1 = 7$ and $14 - 7 = 7$)
7 × 0 = 0 = 7 – 7 (Since $7 \times 0 = 0$ and $7 - 7 = 0$)
7 × – 1 = –7 = 0 – 7 (Since $7 \times (-1) = -7$ and $0 - 7 = -7$)
7 × – 2 = –14 = –7 – 7 (Since $7 \times (-2) = -14$ and $-7 - 7 = -14$)
7 × – 3 = –21 = –14 – 7 (Since $7 \times (-3) = -21$ and $-14 - 7 = -21$)
Question 110. Science Application: An atom consists of charged particles called electrons and protons. Each proton has a charge of +1 and each electron has a charge of –1. Remember number of electrons is equal to number of protons, while answering these questions:
(a) What is the charge on an atom?
(b) What will be the charge on an atom if it loses an electron?
(c) What will be the charge on an atom if it gains an electron?
Answer:
Given:
Charge on each proton = $+1$
Charge on each electron = $-1$
In an atom, number of electrons = number of protons.
To Find:
(a) The charge on an atom.
(b) The charge on an atom if it loses an electron.
(c) The charge on an atom if it gains an electron.
Solution:
(a) What is the charge on an atom?
Let $n$ be the number of protons in an atom.
According to the given information, the number of electrons is also $n$.
Total positive charge from protons = (Number of protons) $\times$ (Charge per proton)
Total positive charge = $n \times (+1) = +n$
Total negative charge from electrons = (Number of electrons) $\times$ (Charge per electron)
Total negative charge = $n \times (-1) = -n$
Total charge on the atom = Total positive charge + Total negative charge
Total charge $= (+n) + (-n) = n - n = 0$
The charge on a neutral atom is 0.
(b) What will be the charge on an atom if it loses an electron?
Assume the atom starts with $n$ protons and $n$ electrons, having a total charge of 0.
If the atom loses one electron, the number of electrons becomes $n - 1$.
The number of protons remains $n$.
Total positive charge = $n \times (+1) = +n$
Total negative charge = $(n - 1) \times (-1) = -(n - 1) = -n + 1$
Total charge on the atom = Total positive charge + Total negative charge
Total charge $= (+n) + (-n + 1) = n - n + 1 = 1$
The charge on the atom will be +1 if it loses an electron.
(c) What will be the charge on an atom if it gains an electron?
Assume the atom starts with $n$ protons and $n$ electrons, having a total charge of 0.
If the atom gains one electron, the number of electrons becomes $n + 1$.
The number of protons remains $n$.
Total positive charge = $n \times (+1) = +n$
Total negative charge = $(n + 1) \times (-1) = -(n + 1) = -n - 1$
Total charge on the atom = Total positive charge + Total negative charge
Total charge $= (+n) + (-n - 1) = n - n - 1 = -1$
The charge on the atom will be -1 if it gains an electron.
Question 111. An atom changes to a charged particle called ion if it loses or gains electrons. The charge on an ion is the charge on electrons plus charge on protons. Now, write the missing information in the table given below:
| Name of Iron | Proton Charge | Electron Charge | Ion Charge |
|---|---|---|---|
| Hydroxide Ion | +9 | ________ | -1 |
| Sodium Ion | +11 | ________ | +1 |
| Aluminium Ion | +13 | -10 | ________ |
| oxide Ion | +8 | -10 | ________ |
Answer:
Solution:
The charge on an ion is given by the sum of the proton charge and the electron charge:
Ion Charge = Proton Charge + Electron Charge
We can use this formula to find the missing information in the table.
Let's fill in the missing values:
Hydroxide Ion:
Given: Proton Charge = $+9$, Ion Charge = $-1$.
Let the Electron Charge be $E$.
Using the formula: $-1 = +9 + E$
Subtract 9 from both sides:
$E = -1 - 9 = -10$
The Electron Charge for Hydroxide Ion is -10.
Sodium Ion:
Given: Proton Charge = $+11$, Ion Charge = $+1$.
Let the Electron Charge be $E$.
Using the formula: $+1 = +11 + E$
Subtract 11 from both sides:
$E = +1 - 11 = -10$
The Electron Charge for Sodium Ion is -10.
Aluminium Ion:
Given: Proton Charge = $+13$, Electron Charge = $-10$.
Let the Ion Charge be $I$.
Using the formula: $I = +13 + (-10)$
$I = 13 - 10 = +3$
The Ion Charge for Aluminium Ion is +3.
Oxide Ion:
Given: Proton Charge = $+8$, Electron Charge = $-10$.
Let the Ion Charge be $I$.
Using the formula: $I = +8 + (-10)$
$I = 8 - 10 = -2$
The Ion Charge for Oxide Ion is -2.
Here is the completed table:
| Name of Ion | Proton Charge | Electron Charge | Ion Charge |
| Hydroxide Ion | +9 | -10 | -1 |
| Sodium Ion | +11 | -10 | +1 |
| Aluminium Ion | +13 | -10 | +3 |
| Oxide Ion | +8 | -10 | -2 |
Question 112. Social Studies Application: Remembering that 1AD came immediately after 1BC, while solving these problems take 1BC as –1 and 1AD as +1.
(a) The Greeco-Roman era, when Greece and Rome ruled Egypt started in the year 330 BC and ended in the year 395 AD. How long did this era last?
(b) Bhaskaracharya was born in the year 1114 AD and died in the year 1185 AD. What was his age when he died?
(c) Turks ruled Egypt in the year 1517 AD and Queen Nefertis ruled Egypt about 2900 years before the Turks ruled. In what year did she rule?
(d) Greek mathematician Archimedes lived between 287 BC and 212 BC and Aristotle lived between 380 BC and 322 BC. Who lived during an earlier period?
Answer:
Given the rule: 1 BC is taken as $-1$ and 1 AD is taken as $+1$. For other BC years, N BC is $-N$. For other AD years, N AD is $+N$. Remembering that 1 AD came immediately after 1 BC.
(a) How long did the Greeco-Roman era last?
Start year = 330 BC
This corresponds to the integer value $-330$.
End year = 395 AD
This corresponds to the integer value $+395$.
Duration of the era is the difference between the end year and the start year.
Duration = End Year Value $-$ Start Year Value
$= 395 - (-330)$
$= 395 + 330$
$= 725$
The Greeco-Roman era lasted for $725$ years.
(b) What was Bhaskaracharya's age when he died?
Born year = 1114 AD
This corresponds to the integer value $+1114$.
Died year = 1185 AD
This corresponds to the integer value $+1185$.
Age when he died is the difference between the died year and the born year.
Age = Died Year Value $-$ Born Year Value
$= 1185 - 1114$
$= 71$
Bhaskaracharya was $71$ years old when he died.
(c) In what year did Queen Nefertis rule?
Turks ruled Egypt in 1517 AD.
This corresponds to the integer value $+1517$.
Queen Nefertis ruled about 2900 years before the Turks ruled.
Year Queen Nefertis ruled = Year Turks ruled value $-$ Number of years before
$= 1517 - 2900$
Let's perform the subtraction:
$\begin{array}{cc} & 2 & 9 & 0 & 0 \\ - & 1 & 5 & 1 & 7 \\ \hline & 1 & 3 & 8 & 3 \\ \hline \end{array}$
So, $1517 - 2900 = -1383$.
A negative year value corresponds to a BC year. Since $-1$ corresponds to 1 BC, $-1383$ corresponds to 1383 BC.
Queen Nefertis ruled in the year 1383 BC.
(d) Who lived during an earlier period, Archimedes or Aristotle?
Archimedes lived between 287 BC and 212 BC.
Using the given rule, this period corresponds to integer values between $-287$ and $-212$.
Aristotle lived between 380 BC and 322 BC.
Using the given rule, this period corresponds to integer values between $-380$ and $-322$.
On the number line, smaller (more negative) numbers represent earlier years.
Comparing the start years: $-380$ and $-287$. Since $-380 < -287$, Aristotle's period started earlier than Archimedes'.
Comparing the end years: $-322$ and $-212$. Since $-322 < -212$, Aristotle's period ended earlier than Archimedes'.
Both the start and end of Aristotle's life occurred at smaller (earlier) year values compared to Archimedes'.
Therefore, Aristotle lived during an earlier period.
Question 113. The table shows the lowest recorded temperatures for each continent. Write the continents in order from the lowest recorded temperature to the highest recorded temperature.
| The Lowest Recorded Temperature | |
|---|---|
| Continent | Temperature |
| Africa | -11$^\circ$ |
| Antartica | -129$^\circ$ |
| Asia | -90$^\circ$ |
| Australia | -9$^\circ$ |
| Europe | -67$^\circ$ |
| North America | -81$^\circ$ |
| South America | -27$^\circ$ |
Answer:
The lowest recorded temperatures for each continent are given in the table:
Africa: $-11^\circ$
Antarctica: $-129^\circ$
Asia: $-90^\circ$
Australia: $-9^\circ$
Europe: $-67^\circ$
North America: $-81^\circ$
South America: $-27^\circ$
To order the continents from the lowest recorded temperature to the highest, we need to arrange the temperatures in ascending order:
$-129^\circ, -90^\circ, -81^\circ, -67^\circ, -27^\circ, -11^\circ, -9^\circ$
Matching the temperatures with their respective continents, the order from lowest to highest temperature is:
$-129^\circ$ (Antarctica)
$-90^\circ$ (Asia)
$-81^\circ$ (North America)
$-67^\circ$ (Europe)
$-27^\circ$ (South America)
$-11^\circ$ (Africa)
$-9^\circ$ (Australia)
Therefore, the continents in order from the lowest recorded temperature to the highest recorded temperature are:
Antarctica, Asia, North America, Europe, South America, Africa, Australia.
Question 114. Write a pair of integers whose product is –12 and there lies seven integers between them (excluding the given integers).
Answer:
We are looking for a pair of integers, let's call them $a$ and $b$, such that:
1. Their product is $-12$. So, $a \times b = -12$.
2. There are exactly seven integers between $a$ and $b$ (excluding $a$ and $b$).
First, let's find pairs of integers whose product is $-12$. Since the product is negative, one integer must be positive and the other must be negative. The possible pairs $(a, b)$ are:
$(1, -12)$
$(-1, 12)$
$(2, -6)$
$(-2, 6)$
$(3, -4)$
$(-3, 4)$
Next, we need to consider the condition that there are seven integers between the pair. Let the two integers be $x$ and $y$, where $x < y$. The number of integers between $x$ and $y$ (exclusive) is given by the formula $y - x - 1$.
We are given that the number of integers between them is $7$.
So, $y - x - 1 = 7$.
Adding 1 to both sides, we get $y - x = 8$.
This means the difference between the larger integer and the smaller integer must be $8$.
Now, let's check the pairs we found for $a \times b = -12$ against the condition $y - x = 8$ (where $y$ is the larger and $x$ is the smaller integer):
1. Pair $(1, -12)$. The smaller integer is $x = -12$ and the larger is $y = 1$.
$y - x = 1 - (-12) = 1 + 12 = 13$.
Number of integers between them $= 13 - 1 = 12$. (Not 7)
2. Pair $(-1, 12)$. The smaller integer is $x = -1$ and the larger is $y = 12$.
$y - x = 12 - (-1) = 12 + 1 = 13$.
Number of integers between them $= 13 - 1 = 12$. (Not 7)
3. Pair $(2, -6)$. The smaller integer is $x = -6$ and the larger is $y = 2$.
$y - x = 2 - (-6) = 2 + 6 = 8$.
Number of integers between them $= 8 - 1 = 7$. (This pair satisfies the condition)
4. Pair $(-2, 6)$. The smaller integer is $x = -2$ and the larger is $y = 6$.
$y - x = 6 - (-2) = 6 + 2 = 8$.
Number of integers between them $= 8 - 1 = 7$. (This pair also satisfies the condition)
5. Pair $(3, -4)$. The smaller integer is $x = -4$ and the larger is $y = 3$.
$y - x = 3 - (-4) = 3 + 4 = 7$.
Number of integers between them $= 7 - 1 = 6$. (Not 7)
6. Pair $(-3, 4)$. The smaller integer is $x = -3$ and the larger is $y = 4$.
$y - x = 4 - (-3) = 4 + 3 = 7$.
Number of integers between them $= 7 - 1 = 6$. (Not 7)
The pairs of integers whose product is $-12$ and which have seven integers between them are $(2, -6)$ and $(-2, 6)$. The question asks for "a pair".
A pair of integers whose product is $-12$ and there lies seven integers between them is $(2, -6)$.
Alternatively, the pair $(-2, 6)$ is also a valid answer.
Question 115. From given integers in Column I match an integer of Column II so that their product lies between –19 and –6:
| Column I | Column II |
|---|---|
| - 5 | 1 |
| 6 | -1 |
| -7 | 3 |
| 8 | -2 |
Answer:
The condition is that the product of an integer from Column I and an integer from Column II must lie between $-19$ and $-6$. This means the product must be greater than $-19$ and less than $-6$, which can be written as: $-19 < \text{Product} < -6$.
Let's find the possible products for each integer in Column I by multiplying it with each integer in Column II and check if the product satisfies the condition.
Consider the integer from Column I: $-5$
Products with integers from Column II:
$-5 \times 1 = -5$
$-5 \times -1 = 5$
$-5 \times 3 = -15$
$-5 \times -2 = 10$
Check the condition $-19 < \text{Product} < -6$:
For product $-5$: Is $-19 < -5 < -6$? No, $-5$ is not less than $-6$.
For product $5$: Is $-19 < 5 < -6$? No, $5$ is not less than $-6$.
For product $-15$: Is $-19 < -15 < -6$? Yes, this is true.
For product $10$: Is $-19 < 10 < -6$? No, $10$ is not less than $-6$.
Match for $-5$ from Column I: $3$ from Column II (product is $-15$).
Consider the integer from Column I: $6$
Products with integers from Column II:
$6 \times 1 = 6$
$6 \times -1 = -6$
$6 \times 3 = 18$
$6 \times -2 = -12$
Check the condition $-19 < \text{Product} < -6$:
For product $6$: Is $-19 < 6 < -6$? No.
For product $-6$: Is $-19 < -6 < -6$? No, $-6$ is not less than $-6$.
For product $18$: Is $-19 < 18 < -6$? No.
For product $-12$: Is $-19 < -12 < -6$? Yes, this is true.
Match for $6$ from Column I: $-2$ from Column II (product is $-12$).
Consider the integer from Column I: $-7$
Products with integers from Column II:
$-7 \times 1 = -7$
$-7 \times -1 = 7$
$-7 \times 3 = -21$
$-7 \times -2 = 14$
Check the condition $-19 < \text{Product} < -6$:
For product $-7$: Is $-19 < -7 < -6$? Yes, this is true.
For product $7$: Is $-19 < 7 < -6$? No.
For product $-21$: Is $-19 < -21 < -6$? No, $-21$ is not greater than $-19$.
For product $14$: Is $-19 < 14 < -6$? No.
Match for $-7$ from Column I: $1$ from Column II (product is $-7$).
Consider the integer from Column I: $8$
Products with integers from Column II:
$8 \times 1 = 8$
$8 \times -1 = -8$
$8 \times 3 = 24$
$8 \times -2 = -16$
Check the condition $-19 < \text{Product} < -6$:
For product $8$: Is $-19 < 8 < -6$? No.
For product $-8$: Is $-19 < -8 < -6$? Yes, this is true.
For product $24$: Is $-19 < 24 < -6$? No.
For product $-16$: Is $-19 < -16 < -6$? Yes, this is true.
Matches for $8$ from Column I: $-1$ from Column II (product is $-8$) and $-2$ from Column II (product is $-16$).
Summary of matches:
For $-5$ from Column I, the match is $3$ from Column II.
For $6$ from Column I, the match is $-2$ from Column II.
For $-7$ from Column I, the match is $1$ from Column II.
For $8$ from Column I, the matches are $-1$ and $-2$ from Column II.
Question 116. Write a pair of integers whose product is – 36 and whose difference is 15.
Answer:
We are asked to find a pair of integers, let's call them $a$ and $b$, such that:
1. Their product is $-36$. So, $a \times b = -36$.
2. Their difference is $15$. Let's assume $b$ is the larger integer and $a$ is the smaller integer. Then $b - a = 15$.
First, let's list the pairs of integers whose product is $-36$. Since the product is negative, one integer must be positive and the other must be negative. The possible factor pairs of 36 are $(1, 36), (2, 18), (3, 12), (4, 9), (6, 6)$.
Considering the negative product, the possible pairs $(a, b)$ where $a < b$ are:
$(-36, 1)$
$(-18, 2)$
$(-12, 3)$
$(-9, 4)$
$(-6, 6)$
$(-4, 9)$
$(-3, 12)$
$(-2, 18)$
$(-1, 36)$
Now, we check the second condition: the difference between the larger integer ($b$) and the smaller integer ($a$) is $15$, i.e., $b - a = 15$.
Let's test each pair $(a, b)$ from the list above:
For $(-36, 1)$: $1 - (-36) = 1 + 36 = 37$. (Not 15)
For $(-18, 2)$: $2 - (-18) = 2 + 18 = 20$. (Not 15)
For $(-12, 3)$: $3 - (-12) = 3 + 12 = 15$. (This pair satisfies the condition)
For $(-9, 4)$: $4 - (-9) = 4 + 9 = 13$. (Not 15)
For $(-6, 6)$: $6 - (-6) = 6 + 6 = 12$. (Not 15)
For $(-4, 9)$: $9 - (-4) = 9 + 4 = 13$. (Not 15)
For $(-3, 12)$: $12 - (-3) = 12 + 3 = 15$. (This pair also satisfies the condition)
For $(-2, 18)$: $18 - (-2) = 18 + 2 = 20$. (Not 15)
For $(-1, 36)$: $36 - (-1) = 36 + 1 = 37$. (Not 15)
The pairs of integers whose product is $-36$ and whose difference is $15$ are $(-12, 3)$ and $(-3, 12)$. The question asks for "a pair".
A pair of integers whose product is $-36$ and whose difference is $15$ is $(-12, 3)$.
Alternatively, the pair $(-3, 12)$ is also a valid answer.
Question 117. Match the following
Column I
(a) $a \times 1$
(b) $1$
(c) $(-a) \div (-b)$
(d) $a \times (-1)$
(e) $a \times 0$
(f) $(-a) \div b$
(g) $0$
(h) $a \div (-a)$
(i) $-a$
Column II
(i) Additive inverse of $a$
(ii) Additive identity
(iii) Multiplicative identity
(iv) $a \div (-b)$
(v) $a \div b$
(vi) $a$
(vii) $-a$
(viii) $0$
(ix) $-1$
Answer:
We need to match each expression or concept in Column I with its equivalent result, property, or concept in Column II.
(a) $a \times 1$
Multiplying any number $a$ by $1$ gives the number itself, $a$.
Looking at Column II, item (vi) is $a$.
Match: (a) $\to$ (vi)
(b) $1$
The number $1$ is the multiplicative identity for integers (and other number systems), meaning $a \times 1 = a$ for any integer $a$.
Looking at Column II, item (iii) is Multiplicative identity.
Match: (b) $\to$ (iii)
(c) $(-a) \div (-b)$
The division of a negative number by a negative number results in a positive number.
$(-a) \div (-b) = \frac{-a}{-b} = \frac{a}{b} = a \div b$.
Looking at Column II, item (v) is $a \div b$.
Match: (c) $\to$ (v)
(d) $a \times (-1)$
Multiplying any number $a$ by $-1$ gives the additive inverse of $a$, which is $-a$.
Looking at Column II, item (vii) is $-a$.
Match: (d) $\to$ (vii)
(e) $a \times 0$
Multiplying any number $a$ by $0$ gives $0$.
Looking at Column II, item (viii) is $0$.
Match: (e) $\to$ (viii)
(f) $(-a) \div b$
The division of a negative number by a positive number results in a negative number. Assuming $b \neq 0$.
$(-a) \div b = \frac{-a}{b} = -\frac{a}{b}$.
This is equivalent to $\frac{a}{-b} = a \div (-b)$.
Looking at Column II, item (iv) is $a \div (-b)$.
Match: (f) $\to$ (iv)
(g) $0$
The number $0$ is the additive identity for integers (and other number systems), meaning $a + 0 = a$ for any integer $a$.
Looking at Column II, item (ii) is Additive identity.
Match: (g) $\to$ (ii)
(h) $a \div (-a)$
For any non-zero integer $a$, dividing $a$ by its additive inverse $-a$ results in $-1$.
$\frac{a}{-a} = -1$, provided $a \neq 0$.
Looking at Column II, item (ix) is $-1$.
Match: (h) $\to$ (ix)
(i) $-a$
The expression $-a$ represents the additive inverse of $a$, because $a + (-a) = 0$ (the additive identity).
Looking at Column II, item (i) is Additive inverse of $a$.
Match: (i) $\to$ (i)
Summary of Matches:
(a) $\to$ (vi)
(b) $\to$ (iii)
(c) $\to$ (v)
(d) $\to$ (vii)
(e) $\to$ (viii)
(f) $\to$ (iv)
(g) $\to$ (ii)
(h) $\to$ (ix)
(i) $\to$ (i)
Question 118. You have ₹ 500 in your savings account at the beginning of the month. The record below shows all of your transactions during the month. How much money is in your account after these transactions?
| Cheque No. | Date | Transaction Description | Payment | Deposit |
|---|---|---|---|---|
| 384102 | 4/9 | Jal Board | $\textsf{₹}$ 120 | |
| 275146 | 12/9 | Deposit | $\textsf{₹}$ 200 | |
| 384103 | 22/9 | LIC India | $\textsf{₹}$ 240 | |
| 801351 | 29/9 | Deposit | $\textsf{₹}$ 150 |
Answer:
Initial balance in the savings account at the beginning of the month = $\textsf{₹} \, 500$.
We will process the transactions in the order they appear in the table and update the balance.
Transaction 1: Cheque No. 384102, Date 4/9, Jal Board payment of $\textsf{₹} \, 120$.
This is a payment, so we subtract this amount from the current balance.
Balance after Transaction 1 = Initial Balance $-$ Payment
$= \textsf{₹} \, 500 - \textsf{₹} \, 120$
$= \textsf{₹} \, 380$
Transaction 2: Cheque No. 275146, Date 12/9, Deposit of $\textsf{₹} \, 200$.
This is a deposit, so we add this amount to the current balance.
Balance after Transaction 2 = Balance after Transaction 1 + Deposit
$= \textsf{₹} \, 380 + \textsf{₹} \, 200$
$= \textsf{₹} \, 580$
Transaction 3: Cheque No. 384103, Date 22/9, LIC India payment of $\textsf{₹} \, 240$.
This is a payment, so we subtract this amount from the current balance.
Balance after Transaction 3 = Balance after Transaction 2 $-$ Payment
$= \textsf{₹} \, 580 - \textsf{₹} \, 240$
$= \textsf{₹} \, 340$
Transaction 4: Cheque No. 801351, Date 29/9, Deposit of $\textsf{₹} \, 150$.
This is a deposit, so we add this amount to the current balance.
Balance after Transaction 4 = Balance after Transaction 3 + Deposit
$= \textsf{₹} \, 340 + \textsf{₹} \, 150$
$= \textsf{₹} \, 490$
After all the transactions are completed, the final amount of money in the account is $\textsf{₹} \, 490$.
Question 119.
(a) Write a positive integer and a negative integer whose sum is a negative integer.
(b) Write a positive integer and a negative integer whose sum is a positive integer.
(c) Write a positive integer and a negative integer whose difference is a negative integer.
(d) Write a positive integer and a negative integer whose difference is a positive integer.
(e) Write two integers which are smaller than – 5 but their difference is – 5.
(f) Write two integers which are greater than – 10 but their sum is smaller than – 10.
(g) Write two integers which are greater than – 4 but their difference is smaller than – 4.
(h) Write two integers which are smaller than – 6 but their difference is greater than – 6.
(i) Write two negative integers whose difference is 7.
(j) Write two integers such that one is smaller than –11, and other is greater than –11 but their difference is –11.
(k) Write two integers whose product is smaller than both the integers.
(l) Write two integers whose product is greater than both the integers.
Answer:
We will provide a pair of integers for each part that satisfies the given conditions.
(a) Write a positive integer and a negative integer whose sum is a negative integer.
Let the positive integer be $p$ and the negative integer be $n$. We want $p + n < 0$. This happens when the absolute value of the negative integer is greater than the absolute value of the positive integer ($|n| > |p|$).
Let's choose the positive integer $3$ and the negative integer $-5$.
Their sum is $3 + (-5) = -2$.
Since $-2$ is a negative integer, the condition is satisfied.
A pair of integers is $3$ and $-5$.
(b) Write a positive integer and a negative integer whose sum is a positive integer.
Let the positive integer be $p$ and the negative integer be $n$. We want $p + n > 0$. This happens when the absolute value of the positive integer is greater than the absolute value of the negative integer ($|p| > |n|$).
Let's choose the positive integer $7$ and the negative integer $-4$.
Their sum is $7 + (-4) = 3$.
Since $3$ is a positive integer, the condition is satisfied.
A pair of integers is $7$ and $-4$.
(c) Write a positive integer and a negative integer whose difference is a negative integer.
Let the positive integer be $p$ and the negative integer be $n$. We want their difference to be a negative integer. If we calculate $n - p$, the result will always be negative since a negative number minus a positive number is always negative.
Let's choose the positive integer $4$ and the negative integer $-2$.
Their difference $(-2) - 4 = -6$.
Since $-6$ is a negative integer, the condition is satisfied.
A pair of integers is $4$ and $-2$.
(d) Write a positive integer and a negative integer whose difference is a positive integer.
Let the positive integer be $p$ and the negative integer be $n$. We want their difference to be a positive integer. If we calculate $p - n$, the result will always be positive since a positive number minus a negative number (which is positive) is always positive.
Let's choose the positive integer $5$ and the negative integer $-3$.
Their difference $5 - (-3) = 5 + 3 = 8$.
Since $8$ is a positive integer, the condition is satisfied.
A pair of integers is $5$ and $-3$.
(e) Write two integers which are smaller than –5 but their difference is –5.
Let the two integers be $a$ and $b$. We need $a < -5$, $b < -5$, and $a - b = -5$ or $b - a = -5$.
Let's try to find $a, b$ such that $a < -5$, $b < -5$ and $a - b = -5$. This means $b = a + 5$.
If $a < -5$, then $a+5 < -5+5 = 0$. So $b$ must be less than $0$. We also need $b < -5$.
Let's pick an integer $a$ that is smaller than $-5$, e.g., $a = -11$.
Then $b = a + 5 = -11 + 5 = -6$.
Check conditions for $a=-11$ and $b=-6$:
$a < -5$? Yes, $-11 < -5$.
$b < -5$? Yes, $-6 < -5$.
Difference $a - b = -11 - (-6) = -11 + 6 = -5$. Yes, the difference is $-5$.
A pair of integers is $-11$ and $-6$.
(f) Write two integers which are greater than –10 but their sum is smaller than –10.
Let the two integers be $a$ and $b$. We need $a > -10$, $b > -10$, and $a + b < -10$.
Let's pick an integer $a$ that is greater than $-10$, e.g., $a = -5$.
We need $b > -10$ and $-5 + b < -10$.
$-5 + b < -10 \implies b < -10 + 5 \implies b < -5$.
So we need an integer $b$ such that $b > -10$ and $b < -5$. An example is $b = -6$.
Check conditions for $a=-5$ and $b=-6$:
$a > -10$? Yes, $-5 > -10$.
$b > -10$? Yes, $-6 > -10$.
Sum $a + b = -5 + (-6) = -11$.
Sum smaller than $-10$? Yes, $-11 < -10$.
A pair of integers is $-5$ and $-6$.
(g) Write two integers which are greater than –4 but their difference is smaller than –4.
Let the two integers be $a$ and $b$. We need $a > -4$, $b > -4$, and $a - b < -4$ or $b - a < -4$.
Let's try to find $a, b$ such that $a > -4$, $b > -4$ and $a - b < -4$.
Let's pick an integer $a$ that is greater than $-4$, e.g., $a = -3$.
We need $b > -4$ and $-3 - b < -4$.
$-3 - b < -4 \implies -b < -4 + 3 \implies -b < -1 \implies b > 1$.
So we need an integer $b$ such that $b > -4$ and $b > 1$. An example is $b = 2$.
Check conditions for $a=-3$ and $b=2$:
$a > -4$? Yes, $-3 > -4$.
$b > -4$? Yes, $2 > -4$.
Difference $a - b = -3 - 2 = -5$.
Difference smaller than $-4$? Yes, $-5 < -4$.
A pair of integers is $-3$ and $2$.
(h) Write two integers which are smaller than –6 but their difference is greater than –6.
Let the two integers be $a$ and $b$. We need $a < -6$, $b < -6$, and $a - b > -6$ or $b - a > -6$.
Let's try to find $a, b$ such that $a < -6$, $b < -6$ and $a - b > -6$.
Let's pick an integer $a$ that is smaller than $-6$, e.g., $a = -7$.
We need $b < -6$ and $-7 - b > -6$.
$-7 - b > -6 \implies -b > -6 + 7 \implies -b > 1 \implies b < -1$.
So we need an integer $b$ such that $b < -6$ and $b < -1$. Both conditions mean $b < -6$.
Let's pick an integer $b$ that is smaller than $-6$, e.g., $b = -8$.
Check conditions for $a=-7$ and $b=-8$:
$a < -6$? Yes, $-7 < -6$.
$b < -6$? Yes, $-8 < -6$.
Difference $a - b = -7 - (-8) = -7 + 8 = 1$.
Difference greater than $-6$? Yes, $1 > -6$.
A pair of integers is $-7$ and $-8$.
(i) Write two negative integers whose difference is 7.
Let the two negative integers be $a$ and $b$. We need $a < 0$, $b < 0$, and $a - b = 7$ or $b - a = 7$.
Let's try to find $a, b$ such that $a < 0$, $b < 0$ and $a - b = 7$. This means $a = b + 7$.
If $b$ is a negative integer, we need $a = b + 7$ to also be a negative integer, which means $b + 7 < 0 \implies b < -7$.
Let's pick a negative integer $b$ that is smaller than $-7$, e.g., $b = -8$.
Then $a = b + 7 = -8 + 7 = -1$.
Check conditions for $a=-1$ and $b=-8$:
$a$ is negative? Yes, $-1 < 0$.
$b$ is negative? Yes, $-8 < 0$.
Difference $a - b = -1 - (-8) = -1 + 8 = 7$. Yes, the difference is $7$.
A pair of negative integers is $-1$ and $-8$.
(j) Write two integers such that one is smaller than –11, and other is greater than –11 but their difference is –11.
Let the two integers be $a$ and $b$. One is $< -11$ and the other is $> -11$. Their difference is $-11$, meaning $a - b = -11$ or $b - a = -11$.
Let's consider the case where the integer smaller than $-11$ is $a$ ($a < -11$) and the integer greater than $-11$ is $b$ ($b > -11$). We need $a - b = -11$. This means $a = b - 11$.
We need $a < -11$ and $b > -11$. Substitute $a = b-11$ into $a < -11$:
$b - 11 < -11 \implies b < -11 + 11 \implies b < 0$.
So we need an integer $b$ such that $b > -11$ and $b < 0$. Examples are $-10, -9, \dots, -1$.
Let's pick $b = -10$.
Then $a = b - 11 = -10 - 11 = -21$.
Check conditions for $a=-21$ and $b=-10$:
One is $< -11$ and the other is $> -11$? Yes, $-21 < -11$ and $-10 > -11$.
Difference $a - b = -21 - (-10) = -21 + 10 = -11$. Yes, the difference is $-11$.
A pair of integers is $-21$ and $-10$.
(k) Write two integers whose product is smaller than both the integers.
Let the two integers be $a$ and $b$. We need $a \times b < a$ and $a \times b < b$.
Consider the integers $2$ and $-1$.
Their product is $2 \times (-1) = -2$.
Is the product smaller than the first integer? $-2 < 2$? Yes.
Is the product smaller than the second integer? $-2 < -1$? Yes.
The condition is satisfied.
A pair of integers is $2$ and $-1$.
(l) Write two integers whose product is greater than both the integers.
Let the two integers be $a$ and $b$. We need $a \times b > a$ and $a \times b > b$.
Consider the integers $2$ and $3$.
Their product is $2 \times 3 = 6$.
Is the product greater than the first integer? $6 > 2$? Yes.
Is the product greater than the second integer? $6 > 3$? Yes.
The condition is satisfied.
Alternatively, consider the integers $-2$ and $-3$.
Their product is $(-2) \times (-3) = 6$.
Is the product greater than the first integer? $6 > -2$? Yes.
Is the product greater than the second integer? $6 > -3$? Yes.
This pair also satisfies the condition.
A pair of integers is $2$ and $3$ (or $-2$ and $-3$).
Question 120. What’s the Error? Ramu evaluated the expression –7 – (–3) and came up with the answer –10. What did Ramu do wrong?
Answer:
Ramu was asked to evaluate the expression: $-7 - (-3)$.
The correct way to evaluate this expression is as follows:
We have $-7$ and we are subtracting $-3$. Subtracting a negative number is the same as adding the corresponding positive number.
So, $-7 - (-3)$ is equivalent to $-7 + 3$.
Now, we add a negative integer $(-7)$ and a positive integer $(3)$. To do this, we find the difference between their absolute values and use the sign of the integer with the larger absolute value.
$|-7| = 7$ and $|3| = 3$.
The difference in absolute values is $7 - 3 = 4$.
The integer with the larger absolute value is $-7$, which is negative.
So, the result is $-4$.
Ramu got the answer $-10$.
Let's consider how one might get $-10$ from this expression. If Ramu treated the expression as $-7 + (-3)$, the result would be $-7 - 3 = -10$.
Alternatively, if Ramu incorrectly subtracted $3$ from $-7$, i.e., $-7 - 3$, the result would also be $-10$.
The error Ramu made was in handling the subtraction of the negative number. He likely misinterpreted $-(-3)$ as $-3$ instead of $+3$. Essentially, he subtracted $3$ from $-7$ (or added $-3$ to $-7$) instead of adding $3$ to $-7$.
Ramu's error was failing to change the sign of the number being subtracted when subtracting a negative integer. He incorrectly calculated $-7 - (-3)$ as $-7 - 3$ (or $-7 + (-3)$) instead of $-7 + 3$.
Question 121. What’s the Error? Reeta evaluated –4 + d for d = –6 and gave an answer of 2. What might Reeta have done wrong?
Answer:
The expression to be evaluated is $-4 + d$ for $d = -6$.
Substituting the value of $d$, the expression becomes:
$-4 + (-6)$
To correctly add two negative integers, we add their absolute values and keep the negative sign.
The absolute value of $-4$ is $|-4| = 4$.
The absolute value of $-6$ is $|-6| = 6$.
Sum of absolute values = $4 + 6 = 10$.
Since both integers are negative, the sum is negative.
So, $-4 + (-6) = -10$.
Reeta got the answer $2$. The correct answer is $-10$.
The magnitude of Reeta's answer is $2$, which is the difference between the absolute values of the two integers ($6 - 4 = 2$). The sign of Reeta's answer is positive, while the correct answer should be negative.
Reeta's likely error was in applying the rule for adding integers with different signs instead of the rule for adding integers with the same sign. When adding two negative integers, one should add their absolute values and make the result negative. Reeta seems to have subtracted the absolute values ($6-4=2$) and possibly made a mistake with the sign, resulting in a positive answer.
Question 122. The table given below shows the elevations relative to sea level of four locations.
Taking sea level as zero, answer the following questions:
| Location | Elevation (in m) |
|---|---|
| A | -180 |
| B | 1600 |
| C | - 55 |
| D | 3200 |
(a) Which location is closest to sea level?
(b) Which location is farthest from sea level?
(c) Arrange the locations from the least to the greatest elevation.
Answer:
The elevations of the four locations relative to sea level (taken as zero) are given in the table:
Location A: $-180$ m
Location B: $1600$ m
Location C: $-55$ m
Location D: $3200$ m
(a) Which location is closest to sea level?
The location closest to sea level is the one with the smallest absolute value of elevation.
The absolute values of the elevations are:
$|-180| = 180$
$|1600| = 1600$
$|-55| = 55$
$|3200| = 3200$
Comparing these absolute values, the smallest value is $55$.
The location with the elevation $-55$ m is Location C.
Therefore, Location C is closest to sea level.
(b) Which location is farthest from sea level?
The location farthest from sea level is the one with the largest absolute value of elevation.
The absolute values of the elevations are $180, 1600, 55, 3200$.
Comparing these absolute values, the largest value is $3200$.
The location with the elevation $3200$ m is Location D.
Therefore, Location D is farthest from sea level.
(c) Arrange the locations from the least to the greatest elevation.
We need to arrange the elevations in ascending order: $-180, 1600, -55, 3200$.
Ordering these numbers from least to greatest:
$-180 < -55 < 1600 < 3200$
Matching these elevations to their locations:
$-180$ m corresponds to Location A.
$-55$ m corresponds to Location C.
$1600$ m corresponds to Location B.
$3200$ m corresponds to Location D.
Therefore, the locations arranged from the least to the greatest elevation are: A, C, B, D.
Question 123. You are at an elevation 380 m above sea level as you start a motor ride. During the ride, your elevation changes by the following metres: 540 m, –268 m, 116 m, –152 m, 490 m, –844 m, 94 m. What is your elevation relative to the sea level at the end of the ride?
Answer:
Initial elevation above sea level = $380$ m.
The changes in elevation during the ride are:
$+540$ m, $-268$ m, $+116$ m, $-152$ m, $+490$ m, $-844$ m, $+94$ m.
A positive change means an increase in elevation, and a negative change means a decrease in elevation.
To find the final elevation, we start with the initial elevation and add each change in elevation.
Elevation after 1st change = $380 + 540 = 920$ m.
Elevation after 2nd change = $920 + (-268) = 920 - 268 = 652$ m.
Elevation after 3rd change = $652 + 116 = 768$ m.
Elevation after 4th change = $768 + (-152) = 768 - 152 = 616$ m.
Elevation after 5th change = $616 + 490 = 1106$ m.
Elevation after 6th change = $1106 + (-844) = 1106 - 844 = 262$ m.
Elevation after 7th change = $262 + 94 = 356$ m.
Alternatively, we can calculate the total change in elevation first by summing all the changes:
Total Change = $540 + (-268) + 116 + (-152) + 490 + (-844) + 94$
Group positive and negative changes:
Positive changes = $540 + 116 + 490 + 94$
$540 + 116 = 656$
$656 + 490 = 1146$
$1146 + 94 = 1240$
Total positive change = $1240$ m.
Negative changes = $(-268) + (-152) + (-844)$
$-268 - 152 - 844$
$-(268 + 152 + 844)$
$268 + 152 = 420$
$420 + 844 = 1264$
Total negative change = $-1264$ m.
Total Change = Total positive change + Total negative change
= $1240 + (-1264)$
= $1240 - 1264$
= $-24$ m.
The total change in elevation is $-24$ m.
Final elevation = Initial elevation + Total Change
= $380$ m $+ (-24)$ m
= $380 - 24$
= $356$ m.
Your elevation relative to the sea level at the end of the ride is $356$ m.
Question 124. Evaluate the following, using distributive property.
(i) – 39 × 99
(ii) (– 85) × 43 + 43 × ( – 15)
(iii) 53 × ( – 9) – ( – 109) × 53
(iv) 68 × (–17) + ( –68) × 3
Answer:
We will evaluate each expression using the distributive property.
(i) $-39 \times 99$
We can write $99$ as $100 - 1$.
Using the distributive property, $a \times (b - c) = a \times b - a \times c$:
$-39 \times 99 = -39 \times (100 - 1)$
$= (-39 \times 100) - (-39 \times 1)$
$= -3900 - (-39)$
$= -3900 + 39$
Now, we add $-3900$ and $39$. The absolute values are $3900$ and $39$. The difference is $3900 - 39 = 3861$. The sign is the sign of the number with the larger absolute value, which is $-3900$, so the result is negative.
$= -3861$
So, $-39 \times 99 = -3861$.
(ii) $(-85) \times 43 + 43 \times (-15)$
This expression is in the form $a \times c + b \times c$, where $a = -85$, $b = -15$, and $c = 43$.
Using the distributive property, $(a + b) \times c = a \times c + b \times c$:
$(-85) \times 43 + 43 \times (-15) = ((-85) + (-15)) \times 43$
$= (-85 - 15) \times 43$
$= (-100) \times 43$
Multiplying $-100$ by $43$:
$= -4300$
So, $(-85) \times 43 + 43 \times (-15) = -4300$.
(iii) $53 \times ( – 9) – ( – 109) \times 53$
We can rewrite the expression. Subtracting a negative number is the same as adding its positive counterpart. So, $- (-109) = +109$.
The expression becomes: $53 \times (-9) + 109 \times 53$.
This is in the form $a \times b + c \times a$, where $a = 53$, $b = -9$, and $c = 109$.
Using the distributive property, $a \times (b + c) = a \times b + a \times c$ (or $a \times b + c \times a = a \times (b + c)$):
$53 \times (-9) + 109 \times 53 = 53 \times ((-9) + 109)$
$= 53 \times (-9 + 109)$
$= 53 \times (100)$
Multiplying $53$ by $100$:
$= 5300$
So, $53 \times ( – 9) – ( – 109) \times 53 = 5300$.
(iv) $68 \times (–17) + ( –68) \times 3$
We can rewrite $-68$ as $68 \times (-1)$.
The expression becomes: $68 \times (-17) + (68 \times (-1)) \times 3$
$= 68 \times (-17) + 68 \times (-1 \times 3)$
$= 68 \times (-17) + 68 \times (-3)$
This is in the form $a \times b + a \times c$, where $a = 68$, $b = -17$, and $c = -3$.
Using the distributive property, $a \times (b + c) = a \times b + a \times c$:
$68 \times (-17) + 68 \times (-3) = 68 \times ((-17) + (-3))$
$= 68 \times (-17 - 3)$
$= 68 \times (-20)$
Multiplying $68$ by $-20$: $68 \times 20 = 1360$. Since one number is positive and the other is negative, the product is negative.
$= -1360$
So, $68 \times (–17) + ( –68) \times 3 = -1360$.
Question 125. If * is an operation such that for integers a and b we have
a * b = a × b + (a × a + b × b)
then find
(i) ( – 3) * (– 5)
(ii) ( – 6) * 2
Answer:
The operation * is defined for integers $a$ and $b$ as:
$a * b = a \times b + (a \times a + b \times b)$
(i) Evaluate $(-3) * (-5)$
Here, $a = -3$ and $b = -5$.
Using the given definition:
$(-3) * (-5) = (-3) \times (-5) + ((-3) \times (-3) + (-5) \times (-5))$
First, calculate the products and squares:
$(-3) \times (-5) = 15$
$(-3) \times (-3) = 9$
$(-5) \times (-5) = 25$
Substitute these values back into the expression:
$(-3) * (-5) = 15 + (9 + 25)$
$= 15 + 34$
$= 49$
So, $(-3) * (-5) = 49$.
(ii) Evaluate $(-6) * 2$
Here, $a = -6$ and $b = 2$.
Using the given definition:
$(-6) * 2 = (-6) \times 2 + ((-6) \times (-6) + 2 \times 2)$
First, calculate the products and squares:
$(-6) \times 2 = -12$
$(-6) \times (-6) = 36$
$2 \times 2 = 4$
Substitute these values back into the expression:
$(-6) * 2 = -12 + (36 + 4)$
$= -12 + 40$
$= 28$
So, $(-6) * 2 = 28$.
Question 126. If ∆ is an operation such that for integers a and b we have
a ∆ b = a × b – 2 × a × b + b × b (–a) × b + b × b
then find
(i) 4 ∆ ( – 3)
(ii) ( – 7) ∆ ( – 1)
Also show that 4 ∆ ( – 3) ≠ (– 3) ∆ 4
and ( – 7) ∆ ( – 1) ≠ ( – 1) ∆ (– 7)
Answer:
The operation $\Delta$ is defined for integers $a$ and $b$ as:
$a \Delta b = a \times b – 2 \times a \times b + b \times b (–a) \times b + b \times b$
Let's simplify the definition of the operation $\Delta$. The term $b \times b (–a) \times b$ means the product of $b^2$, $(-a)$, and $b$.
So, $a \Delta b = (a \times b) - (2 \times a \times b) + (b \times b \times (–a) \times b) + (b \times b)$
$a \Delta b = ab - 2ab - ab^3 + b^2$
$a \Delta b = -ab - ab^3 + b^2$
(i) Find $4 \Delta ( – 3)$
Here, $a = 4$ and $b = -3$.
Using the definition $a \Delta b = -ab - ab^3 + b^2$:
$4 \Delta (-3) = -(4)(-3) - (4)(-3)^3 + (-3)^2$
Calculate the terms:
$-(4)(-3) = -(-12) = 12$
$(-3)^3 = (-3) \times (-3) \times (-3) = 9 \times (-3) = -27$
$(4)(-3)^3 = 4 \times (-27) = -108$
$-(4)(-3)^3 = -(-108) = 108$
$(-3)^2 = (-3) \times (-3) = 9$
Substitute these values back into the expression:
$4 \Delta (-3) = 12 + 108 + 9$
$= 120 + 9$
$= 129$
So, $4 \Delta ( – 3) = 129$.
(ii) Find $( – 7) \Delta ( – 1)$
Here, $a = -7$ and $b = -1$.
Using the definition $a \Delta b = -ab - ab^3 + b^2$:
$(-7) \Delta (-1) = -(-7)(-1) - (-7)(-1)^3 + (-1)^2$
Calculate the terms:
$-(-7)(-1) = -(7) = -7$
$(-1)^3 = (-1) \times (-1) \times (-1) = 1 \times (-1) = -1$
$(-7)(-1)^3 = (-7) \times (-1) = 7$
$-(-7)(-1)^3 = -(7) = -7$
$(-1)^2 = (-1) \times (-1) = 1$
Substitute these values back into the expression:
$(-7) \Delta (-1) = -7 - 7 + 1$
$= -14 + 1$
$= -13$
So, $( – 7) \Delta ( – 1) = -13$.
Show that $4 \Delta ( – 3) \neq (– 3) \Delta 4$
We have already calculated $4 \Delta ( – 3) = 129$.
Now, we need to calculate $(– 3) \Delta 4$.
Here, $a = -3$ and $b = 4$.
Using the definition $a \Delta b = -ab - ab^3 + b^2$:
$(-3) \Delta 4 = -(-3)(4) - (-3)(4)^3 + 4^2$
Calculate the terms:
$-(-3)(4) = -(-12) = 12$
$4^3 = 4 \times 4 \times 4 = 16 \times 4 = 64$
$(-3)(4)^3 = (-3) \times 64 = -192$
$-(-3)(4)^3 = -(-192) = 192$
$4^2 = 4 \times 4 = 16$
Substitute these values back into the expression:
$(-3) \Delta 4 = 12 + 192 + 16$
$= 204 + 16$
$= 220$
We have $4 \Delta ( – 3) = 129$ and $(– 3) \Delta 4 = 220$.
Since $129 \neq 220$, we conclude that $4 \Delta ( – 3) \neq (– 3) \Delta 4$.
Show that $( – 7) \Delta ( – 1) \neq ( – 1) \Delta (– 7)$
We have already calculated $( – 7) \Delta ( – 1) = -13$.
Now, we need to calculate $( – 1) \Delta (– 7)$.
Here, $a = -1$ and $b = -7$.
Using the definition $a \Delta b = -ab - ab^3 + b^2$:
$(-1) \Delta (-7) = -(-1)(-7) - (-1)(-7)^3 + (-7)^2$
Calculate the terms:
$-(-1)(-7) = -(7) = -7$
$(-7)^3 = (-7) \times (-7) \times (-7) = 49 \times (-7) = -343$
$(-1)(-7)^3 = (-1) \times (-343) = 343$
$-(-1)(-7)^3 = -(343) = -343$
$(-7)^2 = (-7) \times (-7) = 49$
Substitute these values back into the expression:
$(-1) \Delta (-7) = -7 - 343 + 49$
$= -350 + 49$
$= -301$
We have $( – 7) \Delta ( – 1) = -13$ and $( – 1) \Delta (– 7) = -301$.
Since $-13 \neq -301$, we conclude that $( – 7) \Delta ( – 1) \neq ( – 1) \Delta (– 7)$.
Question 127. Below u, v, w and x represent different integers, where u = –4 and x ≠ 1. By using following equations, find each of the values:
u × v = u
x × w = w
u + x = w
(a) v
(b) w
(c) x
Explain your reasoning using the properties of integers.
Answer:
We are given the following equations involving integers u, v, w, and x:
$u \times v = u$
... (1)
$x \times w = w$
... (2)
$u + x = w$
... (3)
We are also given that $u = -4$ and $x \neq 1$.
(b) Find the value of w.
Consider the equation $x \times w = w$.
$x \times w = w$
... (2)
Subtract $w$ from both sides of the equation:
$x \times w - w = 0$
Factor out the common term $w$ from the left side:
$w \times (x - 1) = 0$
According to the Zero Product Property, if the product of two integers is zero, then at least one of the integers must be zero. Therefore, either $w = 0$ or $x - 1 = 0$.
If $x - 1 = 0$, then $x = 1$. However, the problem states that $x \neq 1$.
Thus, the only possibility that satisfies the given condition is $w = 0$.
Therefore, the value of w is 0.
(c) Find the value of x.
Now consider the equation $u + x = w$.
$u + x = w$
... (3)
We are given that $u = -4$ and we have found that $w = 0$. Substitute these values into the equation:
$-4 + x = 0$
To solve for $x$, we need to isolate $x$. We can do this by adding the additive inverse of $-4$ to both sides of the equation. The additive inverse of $-4$ is $4$.
$-4 + x + 4 = 0 + 4$
Using the commutative property of addition on the left side, and the Additive Inverse Property (where the sum of an integer and its additive inverse is $0$) and the Additive Identity Property (where adding $0$ to an integer results in the same integer):
$(-4 + 4) + x = 4$
$0 + x = 4$
$x = 4$
The value $x = 4$ is an integer and satisfies the condition $x \neq 1$.
Therefore, the value of x is 4.
(a) Find the value of v.
Consider the equation $u \times v = u$.
$u \times v = u$
... (1)
We are given that $u = -4$. Substitute this value into the equation:
$-4 \times v = -4$
We need to find an integer $v$ such that when $-4$ is multiplied by $v$, the result is $-4$. Since $-4$ is a non-zero integer, this property is related to the multiplicative identity.
According to the property of Multiplicative Identity, multiplying any integer $a$ by $1$ results in $a$ ($a \times 1 = a$). In this case, if $a = -4$, then $-4 \times 1 = -4$.
Comparing $-4 \times v = -4$ with $-4 \times 1 = -4$, we can conclude that $v$ must be $1$.
The value $v = 1$ is an integer.
Therefore, the value of v is 1.
Summary of the values:
(a) v = 1
(b) w = 0
(c) x = 4
We have found integer values for v, w, and x that satisfy all the given equations and conditions, using properties of integers.
Question 128. Height of a place A is 1800 m above sea level. Another place B is 700 m below sea level. What is the difference between the levels of these two places?
Answer:
Given:
Height of place A = $1800$ m above sea level.
Height of place B = $700$ m below sea level.
To Find:
The difference between the levels of these two places.
Solution:
We can represent the elevations relative to sea level using integers, where sea level is $0$ m.
Elevation of place A = $+1800$ m.
Elevation of place B = $-700$ m.
The difference between the levels of the two places is the vertical distance between them. This can be found by subtracting the lower elevation from the higher elevation.
Difference in levels = Elevation of place A $-$ Elevation of place B
$= 1800 - (-700)$
Subtracting a negative integer is the same as adding its positive counterpart:
$= 1800 + 700$
$= 2500$
The difference between the levels of the two places is $2500$ m.
This means place A is $1800$ m above sea level, and place B is $700$ m below sea level. The total vertical distance between them is the sum of the distance from sea level to A ($1800$ m) and the distance from sea level to B ($700$ m below sea level, which is a distance of $700$ m). $1800 + 700 = 2500$ m.
The difference between the levels of the two places is $2500$ m.
Question 129. The given table shows the freezing points in 0F of different gases at sea level. Convert each of these into 0C to the nearest integral value using the relation and complete the table,
$C = \frac{5}{9} (F - 32)$
| Gas | Freezing Point at See Level ($^\circ$F) | Freezing Point at See Level ($^\circ$C) |
|---|---|---|
| Hydrogen | -435 | _________ |
| Krypton | -251 | _________ |
| Oxygen | -369 | _________ |
| Helium | -458 | _________ |
| Argon | -309 | _________ |
Answer:
The relation between Fahrenheit ($^\circ$F) and Celsius ($^\circ$C) is given by the formula:
$C = \frac{5}{9} (F - 32)$
We need to convert the given temperatures in $^\circ$F to $^\circ$C and round to the nearest integral value.
Hydrogen:
Given temperature in $^\circ$F is $-435^\circ$F.
Using the formula:
$C = \frac{5}{9} (-435 - 32)$
$C = \frac{5}{9} (-467)$
$C = \frac{5 \times (-467)}{9}$
$C = \frac{-2335}{9}$
$C \approx -259.44$
Rounding to the nearest integral value, $C \approx -259^\circ$C.
Krypton:
Given temperature in $^\circ$F is $-251^\circ$F.
Using the formula:
$C = \frac{5}{9} (-251 - 32)$
$C = \frac{5}{9} (-283)$
$C = \frac{5 \times (-283)}{9}$
$C = \frac{-1415}{9}$
$C \approx -157.22$
Rounding to the nearest integral value, $C \approx -157^\circ$C.
Oxygen:
Given temperature in $^\circ$F is $-369^\circ$F.
Using the formula:
$C = \frac{5}{9} (-369 - 32)$
$C = \frac{5}{9} (-401)$
$C = \frac{5 \times (-401)}{9}$
$C = \frac{-2005}{9}$
$C \approx -222.78$
Rounding to the nearest integral value, $C \approx -223^\circ$C.
Helium:
Given temperature in $^\circ$F is $-458^\circ$F.
Using the formula:
$C = \frac{5}{9} (-458 - 32)$
$C = \frac{5}{9} (-490)$
$C = \frac{5 \times (-490)}{9}$
$C = \frac{-2450}{9}$
$C \approx -272.22$
Rounding to the nearest integral value, $C \approx -272^\circ$C.
Argon:
Given temperature in $^\circ$F is $-309^\circ$F.
Using the formula:
$C = \frac{5}{9} (-309 - 32)$
$C = \frac{5}{9} (-341)$
$C = \frac{5 \times (-341)}{9}$
$C = \frac{-1705}{9}$
$C \approx -189.44$
Rounding to the nearest integral value, $C \approx -189^\circ$C.
Completed Table:
| Gas | Freezing Point at Sea Level ($^\circ$F) | Freezing Point at Sea Level ($^\circ$C) (nearest integral value) |
| Hydrogen | -435 | -259 |
| Krypton | -251 | -157 |
| Oxygen | -369 | -223 |
| Helium | -458 | -272 |
| Argon | -309 | -189 |
Question 130. Sana and Fatima participated in an apple race. The race was conducted in 6 parts. In the first part, Sana won by 10 seconds. In the second part she lost by 1 minute, then won by 20 seconds in the third part and lost by 25 seconds in the fourth part, she lost by 37 seconds in the fifth part and won by 12 seconds in the last part. Who won the race finally?
Answer:
We are given the time differences for Sana relative to Fatima in each of the 6 parts of the race. We can represent the time Sana is ahead as a negative integer and the time Sana is behind as a positive integer.
The time differences for Sana in each part are:
- Part 1: Won by 10 seconds $\implies -10$ seconds
- Part 2: Lost by 1 minute $\implies +1$ minute
- Part 3: Won by 20 seconds $\implies -20$ seconds
- Part 4: Lost by 25 seconds $\implies +25$ seconds
- Part 5: Lost by 37 seconds $\implies +37$ seconds
- Part 6: Won by 12 seconds $\implies -12$ seconds
To find the total time difference for Sana, we need to sum these values. First, convert all times to seconds:
1 minute = 60 seconds.
The differences in seconds are:
- Part 1: $-10$ seconds
- Part 2: $+60$ seconds
- Part 3: $-20$ seconds
- Part 4: $+25$ seconds
- Part 5: $+37$ seconds
- Part 6: $-12$ seconds
Now, calculate the total difference by summing these values:
Total difference = $(-10) + 60 + (-20) + 25 + 37 + (-12)$
Group the positive and negative numbers:
Positive sum = $60 + 25 + 37 = 122$
Negative sum = $(-10) + (-20) + (-12) = -10 - 20 - 12 = -42$
Total difference = Positive sum + Negative sum
$= 122 + (-42)$
$= 122 - 42$
$= 80$ seconds.
The total time difference for Sana over the 6 parts is $+80$ seconds. This means Sana's total time for the race was 80 seconds more than Fatima's total time.
Since Sana's total time is greater than Fatima's total time, Fatima won the race.
Finally, Fatima won the race.
Question 131. A green grocer had a profit of ₹ 47 on Monday, a loss of ₹ 12 on Tuesday and loss of ₹ 8 on Wednesday. Find his net profit or loss in 3 days.
Answer:
We are given the profit or loss for the green grocer over three days.
Profit is represented by a positive integer, and loss is represented by a negative integer.
Profit on Monday = $\textsf{₹} \, 47$. This is $+47$.
Loss on Tuesday = $\textsf{₹} \, 12$. This is $-12$.
Loss on Wednesday = $\textsf{₹} \, 8$. This is $-8$.
To find the net profit or loss in 3 days, we need to add the amounts for each day:
Net profit/loss = Profit on Monday + Loss on Tuesday + Loss on Wednesday
Net profit/loss = $47 + (-12) + (-8)$
$= 47 - 12 - 8$
We can calculate this step by step:
$47 - 12 = 35$
$35 - 8 = 27$
Alternatively, sum the losses first:
$(-12) + (-8) = -(12 + 8) = -20$
Net profit/loss = $47 + (-20)$
$= 47 - 20$
$= 27$
The net result is $+27$. Since the value is positive, it represents a net profit.
The green grocer's net profit in 3 days is $\textsf{₹} \, 27$.
Question 132. In a test, +3 marks are given for every correct answer and –1 mark are given for every incorrect answer. Sona attempted all the questions and scored +20 marks though she got 10 correct answers.
(i) How many incorrect answers has she attempted?
(ii) How many questions were given in the test?
Answer:
Marks for each correct answer = $+3$
Marks for each incorrect answer = $-1$
Sona attempted all questions and scored $+20$ marks.
Sona got $10$ correct answers.
(i) How many incorrect answers has she attempted?
Let the number of incorrect answers be $n$.
Marks obtained from correct answers = (Number of correct answers) $\times$ (Marks per correct answer)
= $10 \times (+3) = 30$ marks.
Marks obtained from incorrect answers = (Number of incorrect answers) $\times$ (Marks per incorrect answer)
= $n \times (-1) = -n$ marks.
Total score = Marks from correct answers + Marks from incorrect answers
We are given that the total score is $+20$.
$30 + (-n) = 20$
$30 - n = 20$
To find $n$, we can subtract $30$ from both sides of the equation:
$30 - n - 30 = 20 - 30$
$-n = -10$
Multiply both sides by $-1$:
$(-1) \times (-n) = (-1) \times (-10)$
$n = 10$
Sona attempted $10$ incorrect answers.
(ii) How many questions were given in the test?
Sona attempted all the questions.
The total number of questions is the sum of the number of correct answers and the number of incorrect answers.
Number of questions = Number of correct answers + Number of incorrect answers
= $10 + 10$
= $20$
There were $20$ questions given in the test.
Question 133. In a true-false test containing 50 questions, a student is to be awarded 2 marks for every correct answer and –2 for every incorrect answer and 0 for not supplying any answer. If Yash secured 94 marks in a test, what are the possibilities of his marking correct or wrong answer?
Answer:
Given:
Total number of questions in the test = $50$.
Marks for every correct answer = $+2$.
Marks for every incorrect answer = $-2$.
Marks for not supplying any answer = $0$.
Yash's total score = $94$.
To Find:
The possibilities of the number of correct and wrong answers Yash marked.
Solution:
Let $c$ be the number of correct answers.
Let $i$ be the number of incorrect answers.
Let $u$ be the number of unanswered questions.
All $c$, $i$, and $u$ must be non-negative integers ($c \ge 0$, $i \ge 0$, $u \ge 0$).
The total number of questions is $50$. So,
$c + i + u = 50$
... (1)
Yash's total score is the sum of marks from correct, incorrect, and unanswered questions:
Total Score = $(c \times 2) + (i \times -2) + (u \times 0)$
$94 = 2c - 2i + 0$
$2c - 2i = 94$
... (2)
From equation (2), we can divide both sides by $2$:
$\frac{2c - 2i}{2} = \frac{94}{2}$
$c - i = 47$
... (3)
Equation (3) relates the number of correct answers and incorrect answers. We can express $c$ in terms of $i$:
$c = 47 + i$
Now substitute this expression for $c$ into equation (1):
$(47 + i) + i + u = 50$
$47 + 2i + u = 50$
Subtract $47$ from both sides:
$2i + u = 50 - 47$
$2i + u = 3$
... (4)
Now we need to find non-negative integer solutions for $i$ and $u$ in equation (4). We can test possible non-negative integer values for $i$:
Case 1: Let $i = 0$.
Substitute $i=0$ into equation (4):
$2(0) + u = 3$
$0 + u = 3$
$u = 3$
This is a valid non-negative integer for $u$. Now find the corresponding value for $c$ using $c = 47 + i$:
$c = 47 + 0 = 47$
This is a valid non-negative integer for $c$. Let's verify with equation (1): $c + i + u = 47 + 0 + 3 = 50$. This is correct.
Possibility 1: Number of correct answers = $47$, Number of incorrect answers = $0$, Number of unanswered questions = $3$.
Case 2: Let $i = 1$.
Substitute $i=1$ into equation (4):
$2(1) + u = 3$
$2 + u = 3$
Subtract $2$ from both sides:
$u = 3 - 2$
$u = 1$
This is a valid non-negative integer for $u$. Now find the corresponding value for $c$ using $c = 47 + i$:
$c = 47 + 1 = 48$
This is a valid non-negative integer for $c$. Let's verify with equation (1): $c + i + u = 48 + 1 + 1 = 50$. This is correct.
Possibility 2: Number of correct answers = $48$, Number of incorrect answers = $1$, Number of unanswered questions = $1$.
Case 3: Let $i = 2$.
Substitute $i=2$ into equation (4):
$2(2) + u = 3$
$4 + u = 3$
Subtract $4$ from both sides:
$u = 3 - 4$
$u = -1$
This is not a valid non-negative integer for $u$. For any integer $i > 1$, $2i$ will be $4$ or greater, which would result in $u$ being negative in $2i + u = 3$.
Therefore, there are only two possible scenarios for the number of correct and incorrect answers (and consequently, unanswered questions) that result in a score of 94 in a 50-question test with this grading system.
The possibilities for the number of correct and wrong answers are:
Possibility 1: Yash marked 47 correct answers and 0 incorrect answers (leaving 3 unanswered).
Check score: $(47 \times 2) + (0 \times -2) + (3 \times 0) = 94 + 0 + 0 = 94$.
Check total questions: $47 + 0 + 3 = 50$.
Possibility 2: Yash marked 48 correct answers and 1 incorrect answer (leaving 1 unanswered).
Check score: $(48 \times 2) + (1 \times -2) + (1 \times 0) = 96 - 2 + 0 = 94$.
Check total questions: $48 + 1 + 1 = 50$.
Question 134. A multistorey building has 25 floors above the ground level each of height 5m. It also has 3 floors in the basement each of height 5m. A lift in building moves at a rate of 1m/s. If a man starts from 50m above the ground, how long will it take him to reach at 2nd floor of basement?
Answer:
Given:
Height of each floor above ground = 5m.
Number of floors above ground = 25.
Height of each floor in the basement = 5m.
Number of floors in the basement = 3.
Lift speed = 1m/s.
Starting point = 50m above the ground.
Ending point = 2nd floor of basement.
To Find:
Time taken to reach the 2nd floor of the basement from 50m above the ground.
Solution:
We can represent the height above the ground level as positive and the depth below the ground level as negative, taking ground level as 0m.
1. Determine the elevation of the starting point:
The starting point is given as 50m above the ground.
Starting Elevation = $+50$ m.
2. Determine the elevation of the ending point:
The ending point is the 2nd floor of the basement.
Ground level elevation = $0$ m.
Each basement floor has a height of 5m.
The 1st basement floor (B1) is 5m below ground level.
Elevation of B1 = $0 - 5 = -5$ m.
The 2nd basement floor (B2) is 5m below the 1st basement floor.
Elevation of B2 = $-5 - 5 = -10$ m.
Ending Elevation = $-10$ m.
3. Calculate the total vertical distance travelled:
The distance travelled by the lift is the absolute difference between the starting elevation and the ending elevation.
Distance = $| \text{Ending Elevation} - \text{Starting Elevation} |$
= $| -10 - 50 |$
= $| -60 |$
= $60$ m.
4. Calculate the time taken:
The lift moves at a constant speed of 1m/s.
Time taken = $\frac{\text{Distance}}{\text{Speed}}$
= $\frac{60 \text{ m}}{1 \text{ m/s}}$
= $60$ seconds.
It will take the man 60 seconds to reach the 2nd floor of the basement from 50m above the ground.
Question 135. Taking today as zero on the number line, if the day before yesterday is 17 January, what is the date 3 days after tomorrow?
Answer:
We are given that today is represented as $0$ on the number line.
This means:
Today $\leftrightarrow 0$
Tomorrow $\leftrightarrow +1$
The day after tomorrow $\leftrightarrow +2$
Yesterday $\leftrightarrow -1$
The day before yesterday $\leftrightarrow -2$
We are given that the day before yesterday is 17 January.
So, the date corresponding to the number line value $-2$ is 17 January.
To find the date corresponding to today (number line value $0$), we move $0 - (-2) = 2$ days forward from 17 January.
1 day after 17 January is 18 January (corresponds to $-1$).
2 days after 17 January is 19 January (corresponds to $0$).
So, today's date is 19 January.
We need to find the date 3 days after tomorrow.
Tomorrow corresponds to the number line value $+1$.
3 days after tomorrow means we add $3$ to the number line value of tomorrow:
Number line value for 3 days after tomorrow = $+1 + 3 = +4$.
Now we need to find the date corresponding to the number line value $+4$.
Today is 19 January, which corresponds to $0$.
To get to $+4$ from $0$, we move $4 - 0 = 4$ days forward from today.
1 day after today is 20 January (corresponds to $+1$, tomorrow).
2 days after today is 21 January (corresponds to $+2$, day after tomorrow).
3 days after today is 22 January (corresponds to $+3$).
4 days after today is 23 January (corresponds to $+4$, 3 days after tomorrow).
The date 3 days after tomorrow is 23 January.
Question 136. The highest point measured above sea level is the summit of Mt. Everest which is 8,848m above sea level and the lowest point is challenger Deep at the bottom of Mariana Trench which is 10911m below sea level. What is the vertical distance between these two points?
Answer:
Given:
Height of the summit of Mt. Everest above sea level = $8,848$ m
Depth of Challenger Deep below sea level = $10,911$ m
To Find:
The vertical distance between these two points.
Solution:
We can consider sea level as the zero point or reference level ($0$ m).
The position of the summit of Mt. Everest relative to sea level is $+8,848$ m.
The position of Challenger Deep relative to sea level is $-10,911$ m.
The vertical distance between two points is the absolute difference between their positions.
Vertical distance = $| \text{Position of Mt. Everest} - \text{Position of Challenger Deep} |$
$ = | (+8,848) - (-10,911) |$
$ = | 8,848 + 10,911 |$
$ = | 19,759 |$
$ = 19,759$ m
Alternatively, the vertical distance is the sum of the magnitude of the height above sea level and the magnitude of the depth below sea level, as they are on opposite sides of the reference point (sea level).
Vertical distance = Height above sea level + Depth below sea level
$ = 8,848 \text{ m} + 10,911 \text{ m}$
Adding the two distances:
$8,848 + 10,911 = 19,759$
The vertical distance is $19,759$ m.
Final Answer:
The vertical distance between the summit of Mt. Everest and the Challenger Deep is $19,759$ m.

